백준 2565번 문제를 Dynamic Programming(DP, 동적계획법)으로 풀어보았습니다.
백준 2565번: https://www.acmicpc.net/problem/2565
2565번: 전깃줄
첫째 줄에는 두 전봇대 사이의 전깃줄의 개수가 주어진다. 전깃줄의 개수는 100 이하의 자연수이다. 둘째 줄부터 한 줄에 하나씩 전깃줄이 A전봇대와 연결되는 위치의 번호와 B전봇대와 연결되는
www.acmicpc.net
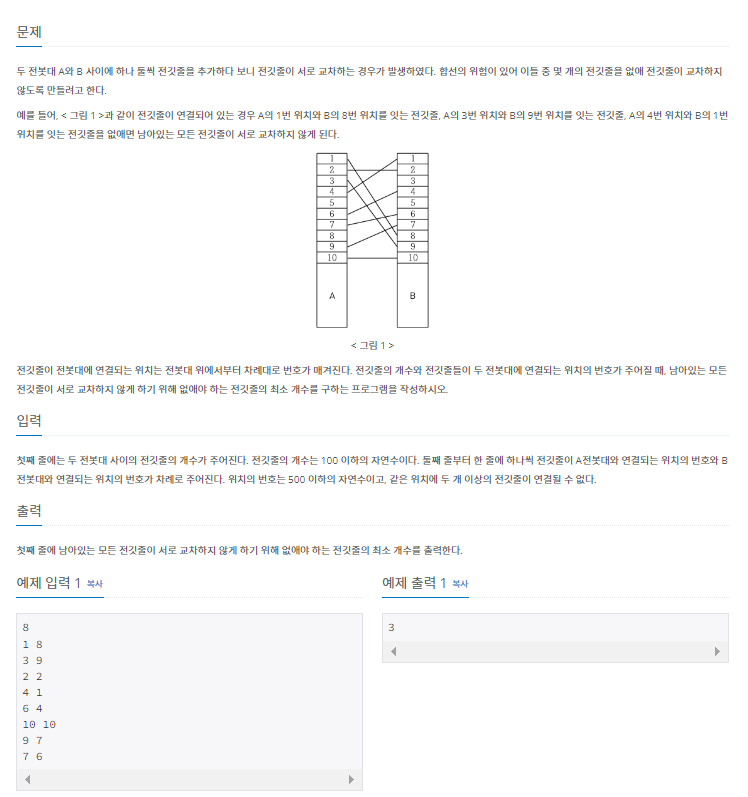
문제 내용은 아래와 같습니다.
목표했던 문제가 있어 동적계획법 공부를 시작하였는데, 목표했던 문제는 이미 해결했으나, 한 번 공부를 시작한 만큼 다른 문제들도 풀어보고 싶어서 이 문제를 골랐습니다. 동적계획법을 공부하고 싶으신 분들은 제 블로그에 관련된 문제를 푼 게시글이 있으니 참고해 주시기 바랍니다. 동적계획법은 많이 접해보고, 나중에는 해당 문제가 동적계획법인지 모르고 접해도 점화식을 통해 풀어야겠다는 판단이 서는 것이 중요하다고 합니다. 따라서 저는 이번 기회에 동적계획법으로 풀 수 있는 예제를 최대한 많이 접해보려고 합니다.
이 문제에 경우 제가 이전에 풀었던 백준 11053번, 가장 긴 증가하는 수열 문제를 먼저 푸시고 접근하시면 더 쉽게 해결하실 수 있습니다. 아래에 해당 문제를 푼 게시글 링크를 추가할 테니 참고해 주세요.
백준 11053번 [가장 긴 증가하는 부분 수열]: https://programming-diary-ina.tistory.com/12
[백준 11053번/C언어] 가장 긴 증가하는 부분 수열, 동적계획법으로 풀이
백준 11053번 문제를 Dynamic Programming (DP, 동적 계획법)으로 풀어보았습니다. 백준 11053번: https://www.acmicpc.net/problem/11053 11053번: 가장 긴 증가하는 부분 수열 수열 A가 주어졌을 때, 가장 긴 증가하는
programming-diary-ina.tistory.com
사실 기본적으로 위 문제의 코드에서 앞 뒤로 기능 한 두 가지 정도 추가하는 것이라고 생각하면 쉽습니다. 우선 A전봇대의 위치 번호를 순서대로 정렬해 준 후에, 같이 정렬된 B전봇대의 위치 번호에서 가장 긴 증가하는 부분 수열을 찾고, 그 수열의 길이를 전깃줄의 총개수에서 빼주면 없애야 하는 전깃줄의 최소 개수가 됩니다.
조금 더 풀어서 설명해보겠습니다. 저는 우선 문제를 접하자마자 "어떻게 하면 전깃줄이 교차하는가"를 파악했습니다. 모두들 쉽게 파악하실 수 있겠지만 전깃줄은
1. A전봇대의 위치값이 더 큰데, B전봇대의 위치값은 더 작을 때
2. A전봇대의 위치값이 더 작은데, B전봇대의 위치값은 더 클 때
위 두 가지 경우에 교차하게 됩니다. 결국 A를 A 전봇대의 위치값, B를 B전봇대의 위치값이라고 하면, 전깃줄이 교차하지 않게 하기 위해서는, A1 < A2이면 B1 < B1이어야 하고, A1 > A2이면 B1 > B2이어야 합니다.
결국, A전봇대의 위치값을 오름차순으로 정리하게 되면 B전봇대의 위치값도 오름차순이어야 전깃줄이 교차하지 않는다는 뜻입니다. 그렇다면 오름차순에 방해되는 전깃줄을 제거하면 될 것입니다. 결과적으로 A전봇대 위치값을 오름차순으로 정리한 후의 B전봇대 전깃줄 배열에서 가장 긴 증가하는 수열을 전체 전깃줄 개수에서 빼주면 제거해야 하는 전깃줄의 최솟값이 됩니다.
그렇다면 점화식을 세워봅시다. 위에 링크를 첨부하긴 했으나, 가장 긴 증가하는 수열의 원소 개수를 구하는 점화식부터 보겠습니다.
F(n) = Max(F(x) ((x < n) && (B[x]< B[n]) + 1
위 점화식에서 F(n)의 최댓값을 찾으면, 해당 값이 가장 긴 증가하는 수열의 원소의 개수가 됩니다.
그리고 최종적으로 우리가 원하는 제거할 전깃줄의 최솟값을 찾기 위해서는 주어진 총 전깃줄 개수에서 위 점화식으로 구한 F(n)의 최댓값을 빼주면 됩니다.
점화식으로 바탕으로 구현한 코드는 다음과 같습니다. 위에서는 정렬 후의 알고리즘에 집중하여 점화식을 설명했기 때문에 정렬 방법에 대해서 언급하지 않아, 여기서 언급하도록 하겠습니다. 우선 아시다시피 C언어는 따로 정렬해 주는 함수가 없기 때문에 직접 정렬 알고리즘을 짜야하고, 여기서는 또 특수하게 단순히 하나의 배열을 정렬하는 것이 아니라, A전봇대 위치값 배열을 정렬함에 따라 B 전봇대 위치값이 어떻게 정렬되는지의 정보가 필요합니다. 정렬 알고리즘을 짜기에도 너무 시간 소요가 클 것 같고, 특수한 방식이 정렬이 필요한 만큼 최적의 방식을 고민한 끝에 고안한 방식은 입력의 최댓값에 맞는 길이의 배열을 만들어 index값을 A 전봇대 위치값으로 사용하고 element를 B 전봇대 위치값으로 하는 것입니다.
그런데 이렇게 두면 중간에 빈 값이 많아 아무래도 정렬 후 알고리즘을 적용하는 것에 어려움을 겪을 것입니다. 따라서 이를 다시 같은 배열에 0에서 n-1까지 index에 저장하여 빈 공간 없이 저장합니다. 이렇게 하면 A 전봇대 위치값 정렬에 따라 바뀐 순서의 B 전봇대의 위치값 배열을 깔끔하게 빼올 수 있습니다.
같은 배열을 사용한 이유는 그저 메모리를 아끼기 위함이었습니다. 이후에 다시 빈 공간이 있는 배열을 쓸 일이 없고, 또 빈 공간이 있는 배열에서 사용할 인덱스의 최소값은 1이지만 빈 공간을 뺀 배열은 0부터 시작하기 때문에, 빈 공간이 있는 배열 요소가 재정렬되기 전 덮어씌워지는 경우도 없을 것입니다. 또한, 뒤쪽에 마구 엉킨 값들이나 빈 공간은 n이라는 총개수를 정확히 파악하고 있으므로, 다시 쓰는 실수만 범하지 않는다면 문제 될 것이 없습니다. (대부분의 반복문을 n-1까지만 반복하도록 해두었으므로, 결과적으로 잘 작동했습니다.)
#include <stdio.h>
#include <stdlib.h>
int main() {
int n;
int line[501] = {0, };
scanf("%d", &n);
int x, y; // A전봇대와 B전봇대 위치값
// 정렬을 위한 빈 공간이 있는 배열 채워넣기
for (int i = 0; i < n; i++) {
scanf("%d %d", &x, &y);
line[x] = y;
}
// 빈 공간을 제거하기 위한 배열 재정렬
int count = 0;
for (int i = 1; i <= 500; i++) {
if (line[i] > 0) {
line[count] = line[i];
count++;
if (count == n) break;
}
}
// 가장 긴 증가하는 수열 알고리즘
int *ascending = (int *)malloc(sizeof(int) * n);
ascending[0] = 1;
int max, res = 0;
for (int i = 0; i < n; i++) {
max = 0;
for (int j = 0; j < i; j++) {
if ((line[i] > line[j]) && (ascending[j] > max)) max = ascending[j];
}
ascending[i] = max + 1;
// 증가하는 수열 중 최댓값 찾기
if (ascending[i] > res) res = ascending[i];
}
printf("%d", n-res); // 결괏값으로 총 전깃줄 개수에서 가장 긴 증가하는 수열 뺀 값 출력
free(ascending);
}'기초 공부 (언어 및 알고리즘) > 알고리즘 (C언어)' 카테고리의 다른 글
| [백준 1920번/C언어] 수 찾기, 이진탐색으로 풀이 (2) | 2023.12.17 |
|---|---|
| [백준 1912번/C언어] 연속합, 동적계획법으로 풀기 (1) | 2023.12.15 |
| [백준 11054번/C 언어] 가장 긴 바이토닉 부분 수열, 동적계획법으로 풀이 (1) | 2023.12.14 |
| [백준 11053번/C언어] 가장 긴 증가하는 부분 수열, 동적계획법으로 풀이 (2) | 2023.12.14 |
| [백준 2156번/C언어] 포도주 시식, 동적계획법으로 풀이 (2) | 2023.12.11 |