[백준 11053번/C언어] 가장 긴 증가하는 부분 수열, 동적계획법으로 풀이

백준 11053번 문제를 Dynamic Programming (DP, 동적 계획법)으로 풀어보았습니다. 

백준 11053번: https://www.acmicpc.net/problem/11053

11053번: 가장 긴 증가하는 부분 수열

 

문제 내용은 아래와 같습니다. 

 

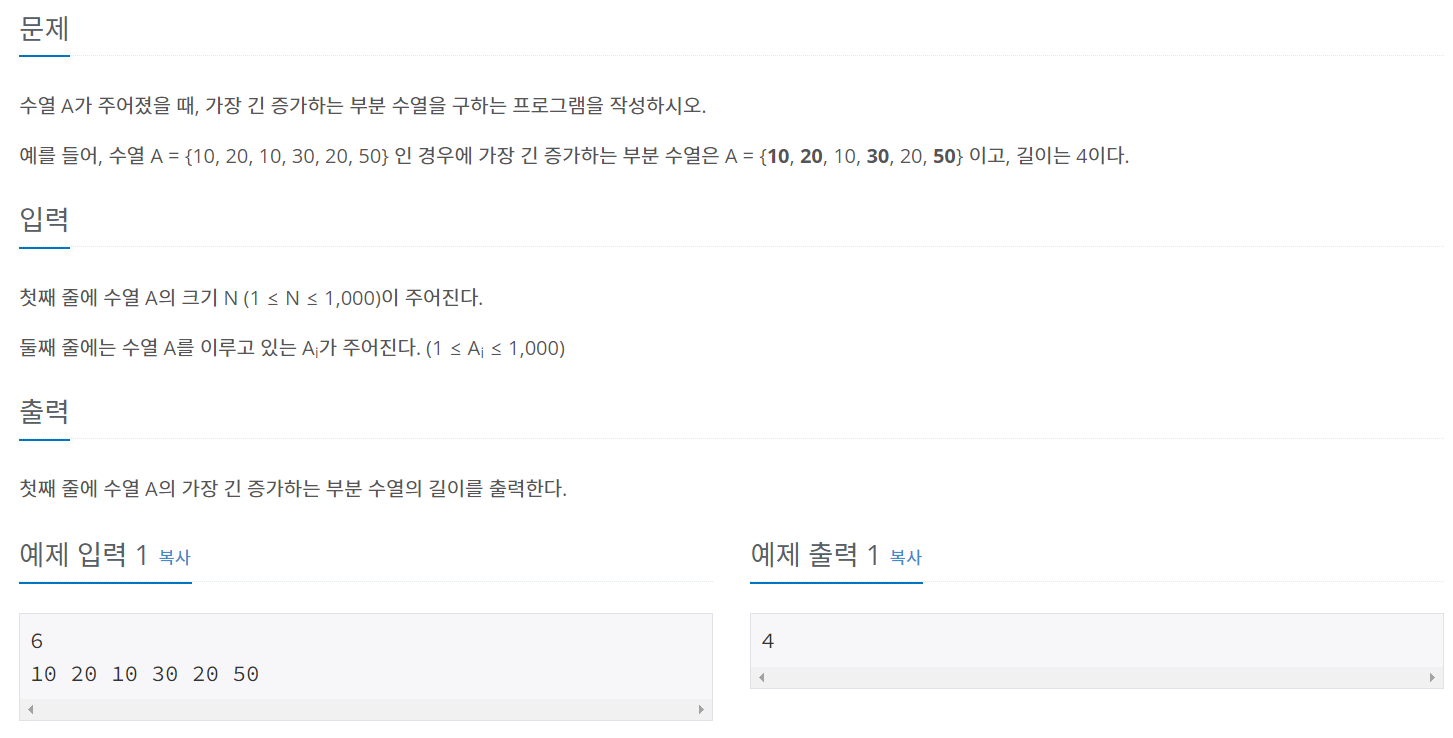
목표했던 문제가 있어 동적계획법 공부를 시작하였는데, 목표했던 문제는 이미 해결했으나, 한 번 공부를 시작한 만큼 다른 문제들도 풀어보고 싶어서 이 문제를 골랐습니다. 동적계획법을 공부하고 싶으신 분들은 제 블로그에 관련된 문제를 푼 게시글이 있으니 참고해 주시기 바랍니다. 동적계획법은 많이 접해보고, 나중에는 해당 문제가 동적계획법인지 모르고 접해도 점화식을 통해 풀어야겠다는 판단이 서는 것이 중요하다고 합니다. 따라서 저는 이번 기회에 동적계획법으로 풀 수 있는 예제를 최대한 많이 접해보려고 합니다. 

하지만 이 문제의 경우, 이전에 풀었던 동적계획법 문제들에 비해 난이도가 높았고, 접근 방식도 독특하다고 느꼈습니다. 그래서 문제를 고민하는데만 많은 시간을 투자한 것 같습니다. 결국에는 다른 블로그를 통해 힌트를 얻어 풀게 되었습니다. 아래는 제가 해당 문제를 풀 때 참고한 블로그입니다. 제 블로그보다 더 상세하게 그림과 함께 설명되어 있으니, 참고하시면 좋을 것 같습니다. 다만 파이썬 풀이라서, C언어를 기대하시고 들어오신 분들은 알고리즘 파악에 해당 블로그를 보시고, 해당 알고리즘을 구현한 코드를 제 블로그로 파악하시면 좋을 것 같습니다. 저는 코드까지 상세히 보고 싶지 않고, 간단한 힌트만 얻고 싶어서 일부러 다른 언어를 사용한 블로그를 참고했습니다. 

https://thingjin.tistory.com/entry/%EB%B0%B1%EC%A4%80-11053%EB%B2%88-%EA%B0%80%EC%9E%A5-%EA%B8%B4-%EC%A6%9D%EA%B0%80%ED%95%98%EB%8A%94-%EB%B6%80%EB%B6%84-%EC%88%98%EC%97%B4-%ED%8C%8C%EC%9D%B4%EC%8D%AC

백준 11053번 가장 긴 증가하는 부분 수열 파이썬

 

우선, 동적계획법으로 푸는 문제인만큼 점화식을 먼저 파악해야 합니다. 이 문제에서 점화식을 파악하는 것이 개인적으로 정말 쉽지 않았습니다. 일단 점화식을 파악하고 나면, 코드를 구현하는 것은 크게 문제가 되지 않습니다. 하지만 규칙을 찾았다 싶으면, 점화식이 아니라는 확신이 설 정도로 반복이 많거나, 예외가 너무 많고 복잡해서 몇 번이고 점화식을 다시 세워야 했습니다. 사실 동적계획법 문제라는 인식 없이 접근했으면, 점화식을 찾아야겠다는 생각도 못했을 것 같습니다.

이렇게 여러 번의 시도 끝에 파악한 점화식을 우선 말로 풀어서 설명하자면, 현재 요소보다 앞에 있는 (즉 인덱스가 작은) 그리고 현재 요소보다 작은 요소들의 결괏값 중 max값에 1을 더하면 됩니다. 그리고 현재 요소보다 작은 요소가 없다면 0에 1을 더하여 1이 결괏값이 됩니다. 이렇게 구한 결괏값들 중 최댓값이 최종 정답이 됩니다. 

따라서 점화식을 아래와 같이 표현할 수 있습니다.

 F(n) = Max(F(x) ((x < n) && (A[x]< A[n]) + 1;

그리고 F(n)의 최댓값을 찾으면 해결되는 문제입니다. 

 

위 점화식으 바탕으로 코드를 짜보았습니다. 

#include <stdio.h>
#include <stdlib.h>

int main() {
    int n;
    scanf("%d", &n);
    
    int *A = (int *)malloc(sizeof(int) * n);
    for (int i = 0; i < n; i++) scanf("%d", &A[i]);
    
    int *res = (int *)malloc(sizeof(int) * n);
    res[0] = 1;
    
    int max;
    for (int i = 1; i < n; i++) {
        max = 0; // 초깃값을 0으로 하여, A[i]보다 작은 값이 없으면 res[i]가 1이 되도록
        for (int j = 0; j < i; j++) {
        	// A[i]보다 작은 요소를 가진 res의 최댓값 찾기
            if ((res[j] > max) && (A[i] > A[j])) max = res[j];
        }
        res[i] = max + 1;
    }
    
    // 결괏값들 중 최댓값 찾기
    max = res[0];
    for (int i = 1; i < n; i++) {
        if (max < res[i]) max = res[i];
    }
    printf("%d", max);
    
    free(A);
    free(res);
}

 

 

마지막으로 제가 참고한 반례모음집 링크를 남깁니다. 

https://acmicpc.net/board/view/114371

글 읽기 - 반례 모음집