백준 1920번 문제를 이진탐색(Binary Search)으로 풀어보았습니다.
백준 1920번: https://www.acmicpc.net/problem/1920
1920번: 수 찾기
첫째 줄에 자연수 N(1 ≤ N ≤ 100,000)이 주어진다. 다음 줄에는 N개의 정수 A[1], A[2], …, A[N]이 주어진다. 다음 줄에는 M(1 ≤ M ≤ 100,000)이 주어진다. 다음 줄에는 M개의 수들이 주어지는데, 이 수들
www.acmicpc.net
문제 내용은 아래와 같습니다.
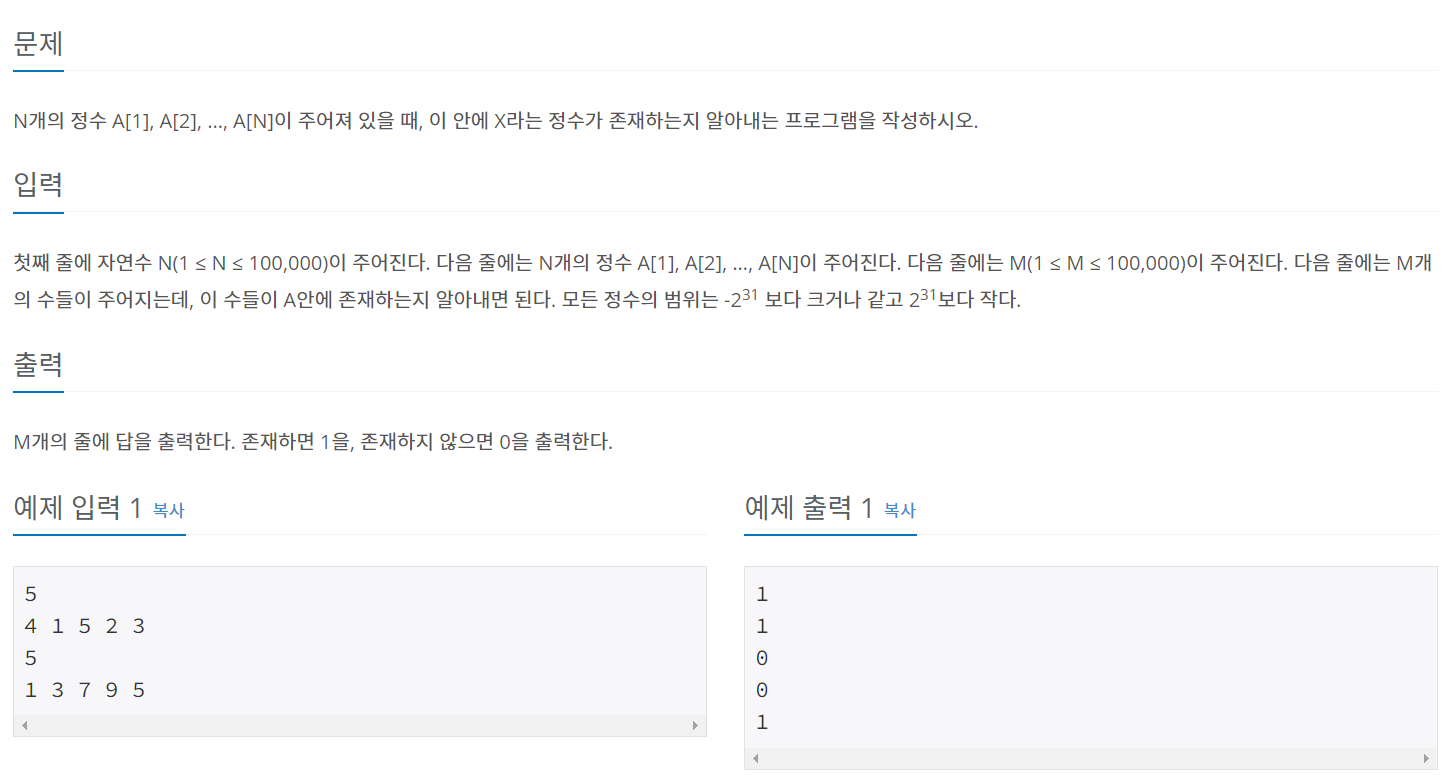
해당 문제를 풀이하면서, 이진탐색트리와 hash table도 사용해 보았으나, 모두 시간 초과로 실패하여 결국 Merge Sort(합병정렬)로 입력받은 배열을 정렬한 후에 Binary Search(이진탐색)를 통해 수를 찾는 방법을 사용하여 해결했습니다.
Merge Sort 알고리즘 관련해서는 아래 글을 참고하시면 되겠습니다. 과거에 푼 문제고 코드를 보고 작성한 것이 아니라 새로 짠 코드이기 때문에 아래 나오는 코드와는 차이가 있을 수 있지만 기본적인 골격은 같기 때문에 내용을 참고하시면 아래 코드도 이해하실 수 있을 것입니다.
[백준 2751번/C언어] 수 정렬하기, Merge Sort로 풀이: https://programming-diary-ina.tistory.com/5
[백준 2751번/C언어] 수 정렬하기, Merge Sort로 풀이
백준 2751번 문제를 Merge Sort로 풀어보았습니다. 처음에는 Quick Sort로 풀이했으나, 계속 정답처리 되지 않아 찾아보니 Quick Sort는 거꾸로 정렬되어 있을 경우 O(N^2)의 시간복잡도가 발생하기 때문에
programming-diary-ina.tistory.com
Binary Search를 사용하기 전에 정렬을 해준 이유는 Binary Search의 전제조건이 배열이 정렬되어야 하는 것이기 때문입니다. 아주 간단한 Binary Search의 예를 보면 다음과 같습니다.
찾으려는 수 n = 5이고 수들이 아래와 같이 정렬되어 있습니다.

위 그림에서 mid 값을 찾으면 2가 되고, mid 위치의 숫자가 n보다 작기 때문에 구간을 오른쪽으로 이동합니다. 왜냐하면 오른쪽 구간의 수들이 현재의 mid 위치의 수보다 모두 클 것이기 때문입니다.
위에서 오른쪽 구간으로 이동한다는 뜻은 mid를 기준으로 반으로 잘라 오른쪽에 해당하는 구간으로 이동한다는 뜻이므로, right 값은 유지되고, left값은 mid+1로 바뀌게 됩니다. 이렇게 해서 다시 중앙값을 찾아주고, 찾으려는 수인 mid와 비교해 주면 탐색에 성공하게 됩니다.
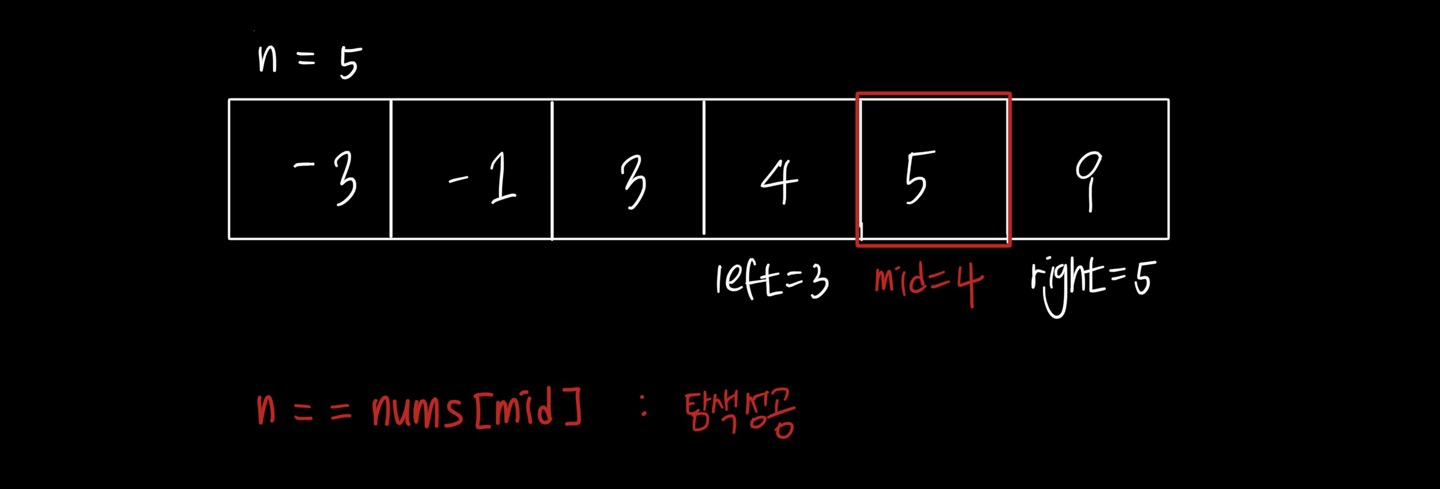
위 예시는 아주 간단한 예시이지만, 확실히 이진탐색의 강점을 알 수 있습니다. 이진탐색을 할 때 우리는 index 4에 위치한 5를 찾기 위해서 단 두 개의 숫자만 확인했습니다. 하지만 만약 선형 탐색을 이용했다면 우리는 index 0부터 4까지 총 5개의 수를 확인하고 나서야 5를 찾을 수 있었을 것입니다.
따라서 이 문제는 선형탐색을 사용하면 시간초과로 실패하게 될 것입니다. n의 최댓값이 100,000이고 m의 최댓값이 100,000이니 최악의 경우 100000^2번을 탐색해야하기 때문입니다. 따라서 보다 효율적인 이진탐색을 위해 시간복잡도를 개선하는 것입니다.
즉, 선형탐색의 경우 한 번 탐색할 때 O(n)의 시간복잡도가 발생하지만, 이진탐색은 O(log n)의 시간복잡도가 발생하므로, 시간복잡도 측면에서 크게 이득이라는 것입니다. 해당 문제는 정렬되어 있지 않은 수들을 입력받으므로, 탐색에 앞서 정렬부터 해야 한다는 불편이 있지만, 합병정렬 역시 시간복잡도가 O(n log n)으로 낮기 때문에, 정렬해야 하는 것을 감안해도 이진탐색이 시간적으로 더 이득이라는 것을 알 수 있습니다.
위에 언급한 알고리즘을 적용하여 구현한 코드는 다음과 같습니다.
#include <stdio.h>
#include <stdlib.h>
void merge(int *nums, int left, int mid, int right) {
if (left == right) return; // left와 right가 같으면 구간 안에 수가 하나 (정렬 필요 X)
if ((right - left) == 1) { // 구간 안에 수가 2개 (둘 끼리만 비교)
if (nums[left] > nums[right]) {
// 왼쪽에 있는 수가 더 클 경우에만 둘 자리를 바꾸기
int temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
}
return;
}
// left ~ mid가 왼쪽 구간, mid+1 ~ right가 오른쪽 구간에 해당
int l = left, r = mid+1; // 각각 왼쪽구간, 오른쪽구간 포인터
int *ordered = (int *)malloc(sizeof(int) * (right - left + 1)); // 정렬된 숫자 저장할 임시 배열
int count = 0; // 임시 배열 저장 위치 파악 용도
while ((l <= mid) && (r <= right)) {
// 왼쪽 구간과 오른쪽 구간 포인터가 가리키는 숫자 중 더 작은 것을 저장하고 저장한 구간 포인터 이동
if (nums[l] < nums[r]) {
ordered[count] = nums[l];
l++;
} else {
ordered[count] = nums[r];
r++;
}
count++;
}
// 왼쪽 구간이나 오른쪽 구간 남은 숫자 저장
while (l <= mid) {
ordered[count] = nums[l];
l++;
count++;
}
while (r <= right) {
ordered[count] = nums[r];
r++;
count++;
}
// 임시 배열에 정렬된 숫자 위치에 맞게 기존 배열에 옮겨넣기
count = 0;
for (int i = left; i <= right; i++) {
nums[i] = ordered[count];
count++;
}
free(ordered);
}
// 재귀를 통해 정렬하는 합병정렬
void mergeSort(int *nums, int left, int right) {
if (left >= right) return;
int mid = (left + right) / 2;
mergeSort(nums, left, mid); // 왼쪽 구간 나누기
mergeSort(nums, mid+1, right); // 오른쪽 구간 나누기
merge(nums, left, mid, right); // 왼쪽 구간 오른쪽 구간 합치기
}
// 정수 n이 nums 배열 안에 존재하면 1, 아니면 0을 return
int search(int n, int l, int r, int *nums) {
if (l == r) {
if (nums[l] == n) return 1;
else return 0;
}
int mid;
while (l < r) {
mid = (l + r) / 2;
if (n == nums[mid]) return 1; // 찾고자하는 n과 중앙값이 같다면 바로 1 return하여 함수 종료
// 찾고자 하는 n이 중앙값보다 작으면 왼쪽 구간으로, 크면 오른쪽 구간으로 이동
if (n < nums[mid]) r = mid;
else l = mid + 1;
}
if ((l == r) && (nums[l] == n)) return 1;
return 0;
}
int main() {
int n;
scanf("%d", &n);
int *nums = (int *)malloc(sizeof(int) * n);
for (int i = 0; i < n; i++) scanf("%d", &nums[i]);
mergeSort(nums, 0, n-1); // 입력받은 배열 정렬
int m, x;
scanf("%d", &m);
for (int i = 0; i < m; i++) {
scanf("%d", &x);
printf("%d\n", search(x, 0, n-1, nums)); // 이진탐색으로 수찾기
}
free(nums);
}
마지막으로 제가 문제를 풀다가 발생했던 반례와 원인을 기록해보려 합니다.
제가 실패했던 반례는 아래와 같습니다.
Input:
4
1 2 3 4
4
1 2 3 4
Answer: 1 1 1 1
Ouput:: 1 1 1 0
반례가 발생한 것을 보고 처음에는 merge sort에 문제가 생긴 줄 알고 sort 후의 배열을 살펴봤으나 문제가 없었습니다. 그래서 다시 문제를 생각해보니, 아래 코드에 문제가 있는 것이었습니다.
// 정수 n이 nums 배열 안에 존재하면 1, 아니면 0을 return
int search(int n, int l, int r, int *nums) {
if (l == r) {
if (nums[l] == n) return 1;
else return 0;
}
int mid;
while (l < r) {
mid = (l + r) / 2;
if (n == nums[mid]) return 1; // 찾고자하는 n과 중앙값이 같다면 바로 1 return하여 함수 종료
// 찾고자 하는 n이 중앙값보다 작으면 왼쪽 구간으로, 크면 오른쪽 구간으로 이동
if (n < nums[mid]) r = mid;
else l = mid + 1;
}
return 0;
}
위 코드는 수정 전 저의 search 함수 입니다. 수정 후 코드와의 차이점은 while문 다음에 아래 코드 한 줄이 빠져있는 것입니다.
if ((l == r) && (nums[l] == n)) return 1;
수정 코드에서는 l==r이면 해당 숫자에 대해 따로 확인하지 않고 바로 while문을 빠져나와, 해당 숫자가 없다는 뜻인 0을 return 합니다. 하지만 위 반례의 4의 경우에는 아래 순서에 따라 nums 배열의 4에 도착하게 됩니다.
[first recursion] left = 0, right = 3, mid = 1
[second recursion] left = 2, right = 3, mid = 2
[third recursion] left = 3, right = 3, mid = 3
하지만 세번째 반복에서 비교 없이 0을 return 하다 보니, 4가 nums 배열 내에 있음에도 없다고 출력하게 되는 것입니다. 따라서 위에서 if문을 추가하여 코드를 완성할 수 있었습니다.
처음에는 while (l <= r)으로 while문을 수정할까도 생각했지만, 그렇게 하면 right = mid가 계속 반복되어 무한 반복 루프가 발생할 수 있기 때문에, if문을 추가하는 것으로 대체했습니다.
'기초 공부 (언어 및 알고리즘) > 알고리즘 (C언어)' 카테고리의 다른 글
| [백준 1654번/C언어] 랜선 자르기, 이진탐색으로 풀이 (0) | 2024.03.15 |
|---|---|
| [백준 9012번/C언어] 괄호 풀이 (1) | 2024.03.15 |
| [백준 1912번/C언어] 연속합, 동적계획법으로 풀기 (1) | 2023.12.15 |
| [백준 2565번/C언어] 전깃줄, 동적계획법으로 풀이 (1) | 2023.12.15 |
| [백준 11054번/C 언어] 가장 긴 바이토닉 부분 수열, 동적계획법으로 풀이 (1) | 2023.12.14 |