백준 11054번 문제를 Dynamic Programming (DP, 동적 계획법)으로 풀어보았습니다.
백준 11054번: https://www.acmicpc.net/problem/11054
11054번: 가장 긴 바이토닉 부분 수열
첫째 줄에 수열 A의 크기 N이 주어지고, 둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (1 ≤ N ≤ 1,000, 1 ≤ Ai ≤ 1,000)
www.acmicpc.net
문제 내용은 아래와 같습니다.
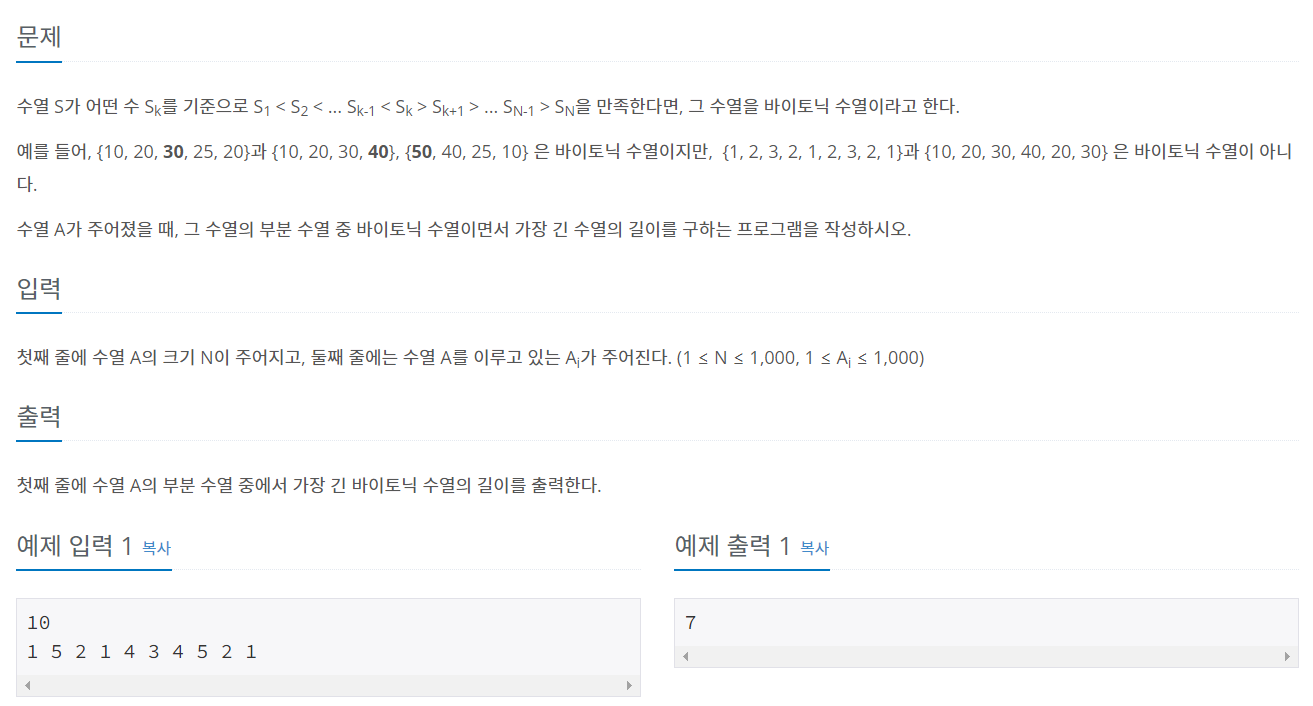
목표했던 문제가 있어 동적계획법 공부를 시작하였는데, 목표했던 문제는 이미 해결했으나, 한 번 공부를 시작한 만큼 다른 문제들도 풀어보고 싶어서 이 문제를 골랐습니다. 동적계획법을 공부하고 싶으신 분들은 제 블로그에 관련된 문제를 푼 게시글이 있으니 참고해 주시기 바랍니다. 동적계획법은 많이 접해보고, 나중에는 해당 문제가 동적계획법인지 모르고 접해도 점화식을 통해 풀어야겠다는 판단이 서는 것이 중요하다고 합니다. 따라서 저는 이번 기회에 동적계획법으로 풀 수 있는 예제를 최대한 많이 접해보려고 합니다.
이 문제에 경우 제가 이전에 풀었던 백준 11053번, 가장 긴 증가하는 수열 문제를 먼저 푸시고 접근하시면 더 쉽게 해결하
실 수 있습니다. 아래에 해당 문제를 푼 게시글 링크를 추가할 테니 참고해 주세요.
백준 11053번 [가장 긴 증가하는 부분 수열]: https://programming-diary-ina.tistory.com/12
[백준 11053번/C언어] 가장 긴 증가하는 부분 수열, 동적계획법으로 풀이
백준 11053번 문제를 Dynamic Programming (DP, 동적 계획법)으로 풀어보았습니다. 백준 11053번: https://www.acmicpc.net/problem/11053 11053번: 가장 긴 증가하는 부분 수열 수열 A가 주어졌을 때, 가장 긴 증가하는
programming-diary-ina.tistory.com
가장 긴 증가하는 부분 수열 문제를 참고하는 이유는, 해당 문제에서 세운 점화식을 한 번, 그리고 거꾸로 한 점화식을 한 번 계산하여 더한 것이 결괏값이 되기 때문입니다.
가장 긴 증가하는 부분 수열 문제에서 세운 점화식은 아래와 같습니다. 현재 요소보다 앞에 있는 (즉 인덱스가 작은) 그리고 현재 요소보다 작은 요소들의 결괏값 중 max값에 1을 더하는 것을 식으로 만든 것입니다.
Left(n) = Max(Left(x) ((x < n) && (A[x]< A[n]) + 1
위 식을 바이토닉 부분 수열의 기준점(수열에서 가장 큰 값)의 왼쪽 부분에 적용하면 됩니다. (마지막에 제시된 코드에서 left 수열을 구하는 것에 해당)
그렇다면 오른쪽 부분의 길이는 어떻게 구하면 될까요? 정확히 반대로 구하면 됩니다. 감소하는 부분 수열의 길이를 구한다고 생각해도 좋습니다. 그렇게 세운 점화식은 아래와 같습니다.
Right(n) = Max(Right(x) ((x > n) && (A[x]< A[n]) + 1
현재 요소보다 작은 요소들의 결괏값을 찾는 것은 같습니다. 하지만 인덱스 값이 더 큰, 즉 현재 요소보다 뒤에 있는 요소들 중에서 찾아야 합니다. 해당 max값에 1을 더해주면 오른쪽 부분의 길이를 구한 수열(마지막 코드에서 right 수열에 해당)도 완성됩니다.
마지막으로 left 부분과 right 부분을 더한 후 1을 뺀 값 중에 가장 큰 값을 찾아 출력해 주면 최종 결괏값이 됩니다. 우선 left 부분과 right 부분을 더한 값 중에 최댓값을 구해준 후 마지막에 1을 빼줘도 되겠죠? 1을 빼주는 이유는 자기 자신이 2번 포함되었기 때문에 둘 중 한 번을 제외해줘야 하기 때문입니다.
위 점화식을 바탕으로 코드를 작성해 보았습니다.
#include <stdio.h>
#include <stdlib.h>
int main() {
int n;
scanf("%d", &n);
int *A = (int *)malloc(sizeof(int) * n);
for (int i= 0; i < n; i++) scanf("%d", &A[i]);
// n이 1일 경우: 자기 자신 하나만 포함하는 수열
// n이 2일 경우: 어느쪽으로든 증가/감소하는 수열이 되므로 길이가 2인 수열
if (n <= 2) {
printf("%d", n);
return 0;
}
// 가장 긴 증가하는 수열 찾기
int *left = (int *)malloc(sizeof(int) * n);
left[0] = 1;
int max;
for (int i = 1; i < n; i++) {
// 자신보다 앞에 있으며 자신보다 작은 요소 중 가장 긴 증가하는 수열을 가지고 있는 요소를 찾아 해당 값에 + 1
max = 0;
for (int j = 0; j < i; j++) {
if ((left[j] > max) && (A[j] < A[i])) max = left[j];
}
left[i] = max + 1;
}
// 가장 긴 감소하는 수열 찾기
int *right = (int *)malloc(sizeof(int) * n);
right[n-1] = 1;
for (int i = n-2; i >= 0; i--) {
// 자신보다 뒤에 있으며 자신보다 작은 요소 중 가장 긴 감소하는 수열을 가지고 있는 요소를 찾아 해당 값에 + 1
max = 0;
for (int j = i+1; j < n; j++) {
if ((right[j] > max) && (A[j] < A[i])) max = right[j];
}
right[i] = max + 1;
}
// 증가하는 수열과 감소하는 수열 (즉, left와 right)를 합쳐 가장 큰 결괏값 찾기
max = 0;
int cur;
for (int i = 0; i < n; i++) {
cur = left[i] + right[i];
if(cur > max) max = cur;
}
// left와 right를 더했을 때 자기자신을 두 번 포함하므로 1 빼준 값이 최종 결괏값
printf("%d", max-1);
free(A);
free(left);
free(right);
}
마지막으로 제가 유용하게 참고했던 반례 모음집 링크를 첨부합니다.
https://www.acmicpc.net/board/view/56223
글 읽기 - 가장 긴 바이토닉 수열 반례 및 필독FAQ 모음
댓글을 작성하려면 로그인해야 합니다.
www.acmicpc.net
'기초 공부 (언어 및 알고리즘) > 알고리즘 (C언어)' 카테고리의 다른 글
| [백준 1912번/C언어] 연속합, 동적계획법으로 풀기 (1) | 2023.12.15 |
|---|---|
| [백준 2565번/C언어] 전깃줄, 동적계획법으로 풀이 (1) | 2023.12.15 |
| [백준 11053번/C언어] 가장 긴 증가하는 부분 수열, 동적계획법으로 풀이 (2) | 2023.12.14 |
| [백준 2156번/C언어] 포도주 시식, 동적계획법으로 풀이 (2) | 2023.12.11 |
| [백준 1463번/C언어] 1로 만들기, 동적계획법으로 풀이 (0) | 2023.12.11 |