백준 2751번 문제를 Merge Sort로 풀어보았습니다.
처음에는 Quick Sort로 풀이했으나, 계속 정답처리 되지 않아 찾아보니 Quick Sort는 거꾸로 정렬되어 있을 경우 O(N^2)의 시간복잡도가 발생하기 때문에 시간초과로 인한 오답이라는 정보를 얻게 되었습니다.
따라서 이를 보완하고자 Merge Sort로 풀이하여 최종적으로 정답처리될 수 있었습니다.
백준 2751번: https://www.acmicpc.net/problem/2751
2751번: 수 정렬하기 2
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)이 주어진다. 둘째 줄부터 N개의 줄에는 수가 주어진다. 이 수는 절댓값이 1,000,000보다 작거나 같은 정수이다. 수는 중복되지 않는다.
www.acmicpc.net
문제 내용은 아래와 같습니다. 예제 입출력이 하나밖에 준비되어있지 않으나, 정렬 문제인 만큼 스스로 예제 입출력을 추가하여 쉽게 본인의 코드를 확인할 수 있을 것으로 보입니다.

코드를 구성하기 전, Merge Sort에 대해서 먼저 공부했습니다. 이전에 이미 수업을 통해 배웠던 내용이라 간단히 복습만 했습니다. 간단히 정리하면, 배열을 가장 작은 단위까지 쪼개었다가 다시 합치면서 정렬을 하는 알고리즘입니다.
백준 문제에 제시된 예제를 그림으로 표현하면서 설명해보겠습니다.
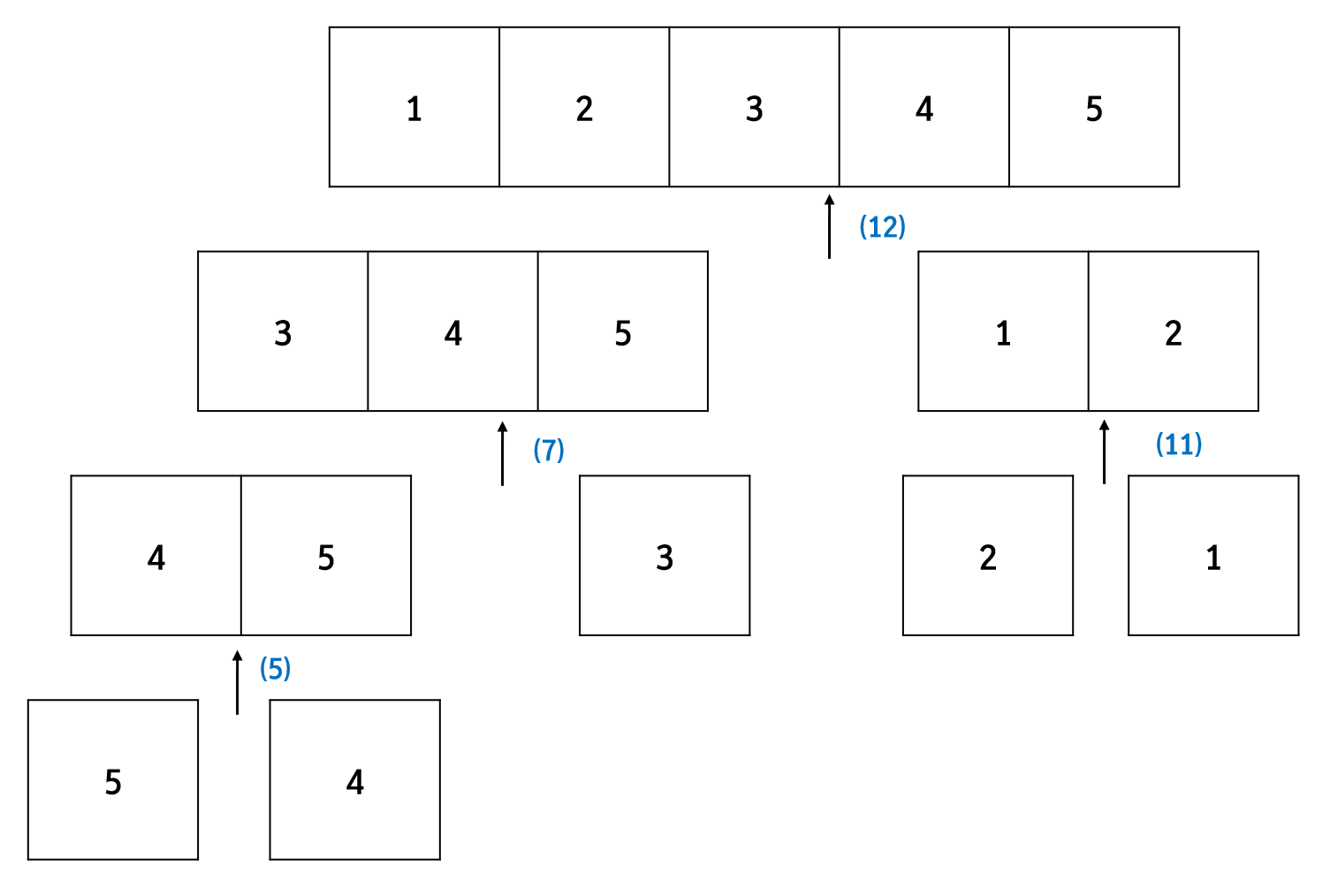
아래와 같이 크기가 5인 배열을 원소 하나하나로 쪼개는 것으로 시작합니다. 추후 나올 코드에서는 이것을 재귀함수를 통해 구현합니다.
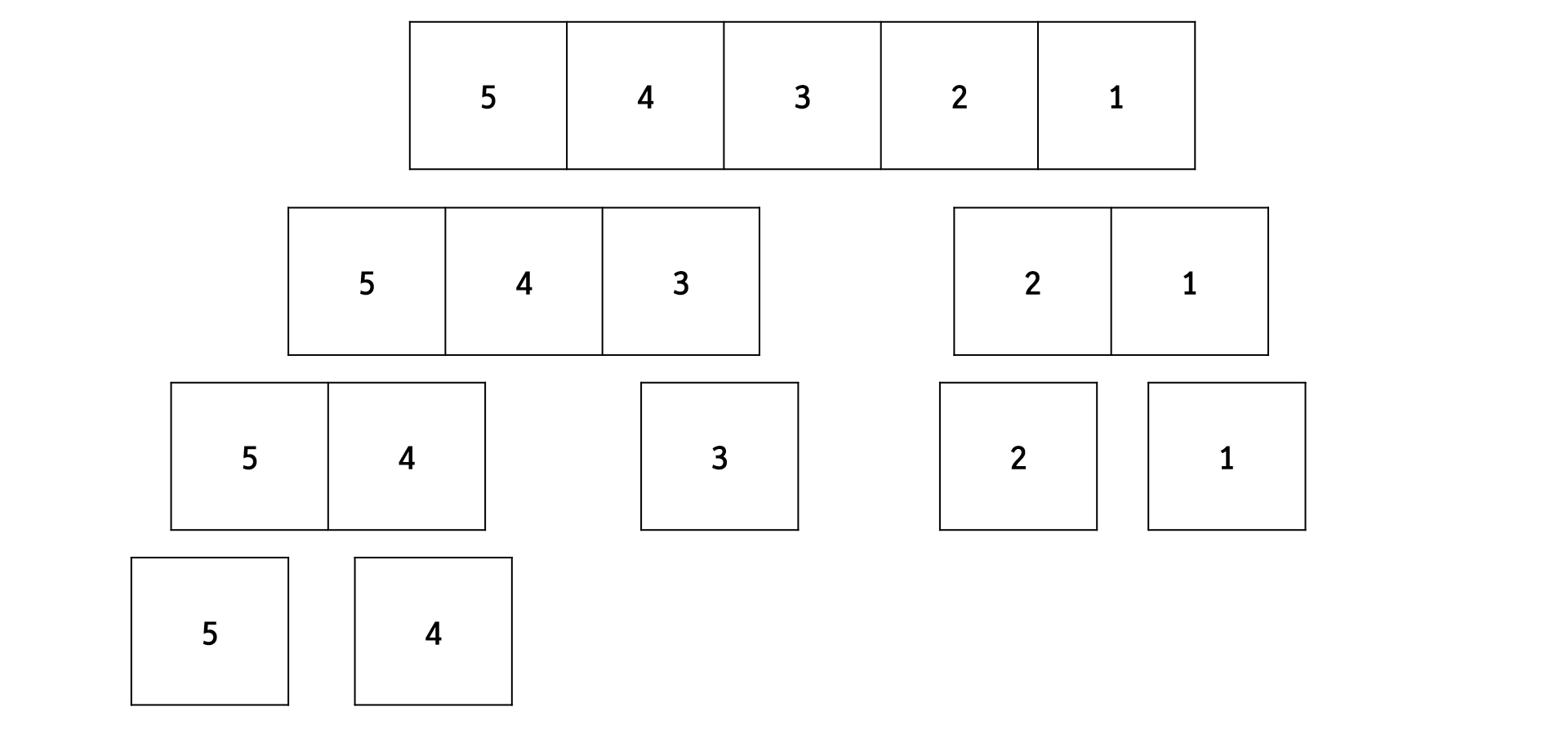
다음은 쪼개진 배열을 합치는 과정인데요, 이를 merge라고 부르고 이 과정 때문에 해당 정렬 알고리즘에 Merge Sort라는 이름이 붙은 것이라고 할 수 있습니다. 아래는 예시를 조금 쉽게 들기 위해서 마지막 merge 과정을 가져왔습니다. 우선 대상이 되는 nums 배열의 크기에 맞는 빈 배열 하나를 생성합니다.
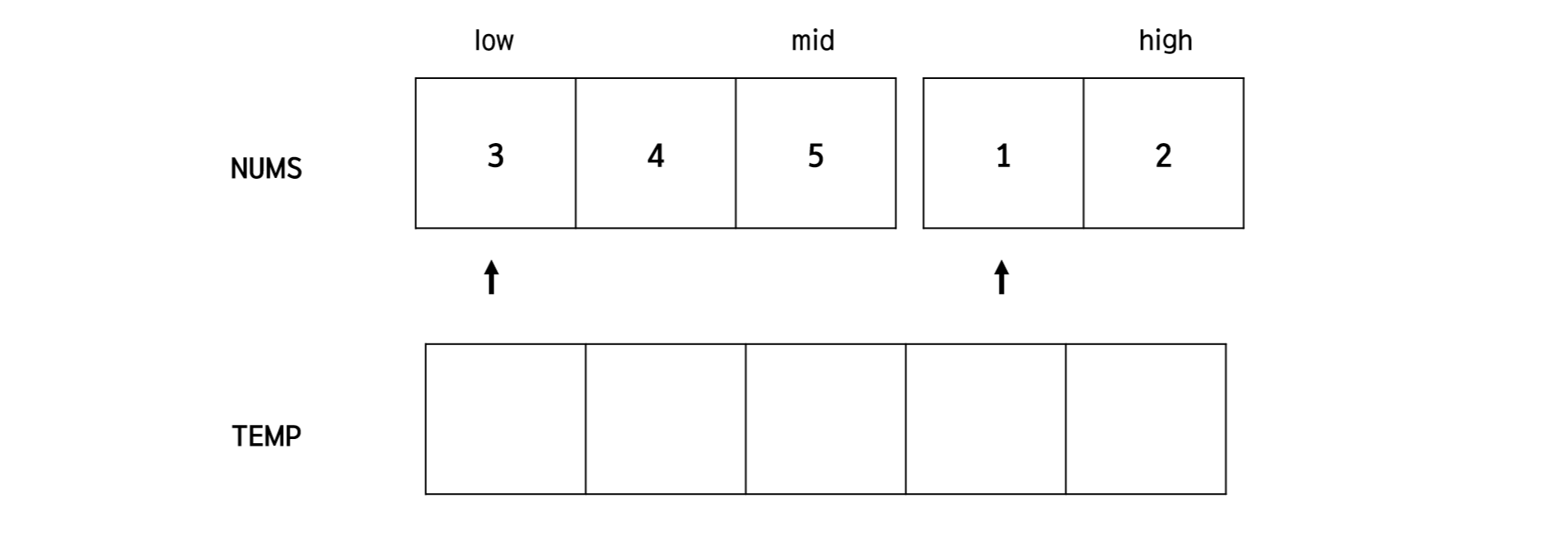
그러고 나서는 아래 그림과 같이 화살표가 가리키는 배열 요소 중 더 작은 요소를 빈 배열에 넣고 화살표를 하나 옮기는 과정을 반복합니다.
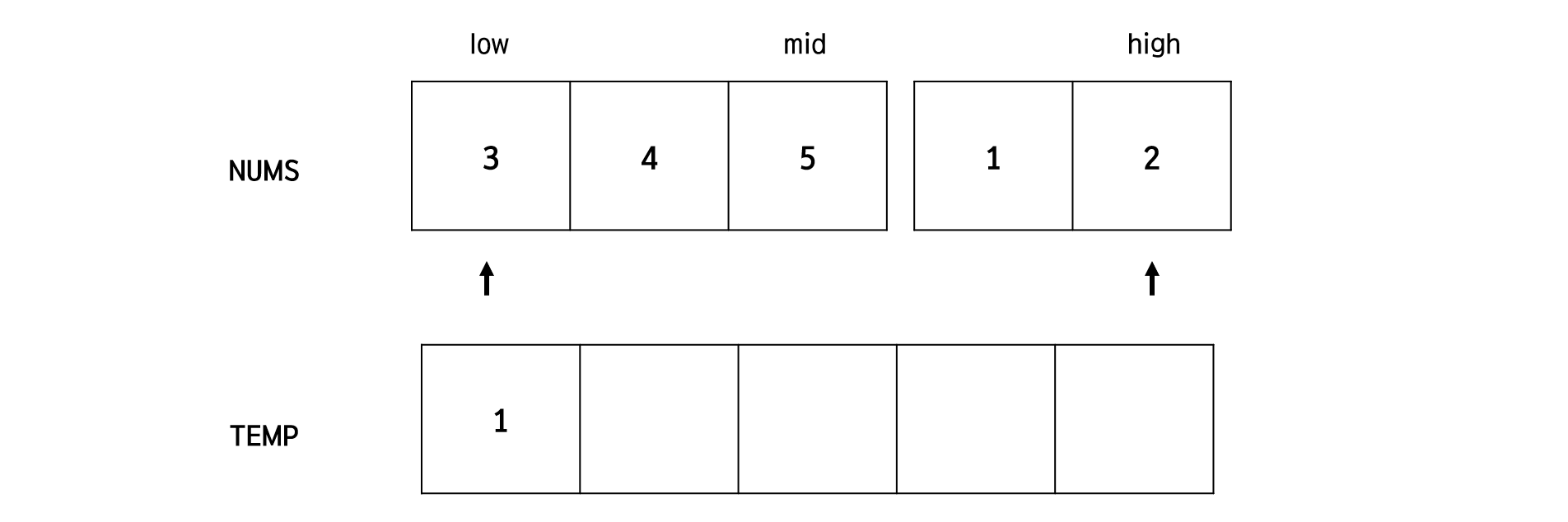
위에서 말한 반복 과정을 종료하면 아래와 같은 그림이 되겠네요. 그럼 이제 Temp 배열에 있는 정렬된 숫자를 다시 Nums 배열에 넣는 것으로 과정이 마무리됩니다. 이렇게 그림과 같이 merge가 종료되면 해당하는 부분은 정렬이 완료되게 되는데요, 왜냐하면 이전 과정에서 이미 더 작은 단위를 정렬해 둔 상태이기 때문입니다.

Merge 정렬에 대한 더 자세한 설명을 원하신다면 아래 글을 참고하시기 바랍니다. 저는 이렇게 간단하게 복습 개념으로 정리하고 바로 코드를 짜보도록 하겠습니다.
https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html
[알고리즘] 합병 정렬(merge sort)이란 - Heee's Development Blog
Step by step goes a long way.
gmlwjd9405.github.io
위와 같은 내용의 Merge Sort를 적용하여 아래와 같은 코드를 구성해보았습니다.
#include <stdio.h>
#include <stdlib.h>
void merge(int *nums, int low, int mid, int high) {
if (low >= high) return; // 해당 구역 요소가 하나 (정렬 필요 없음)
else if (low == mid) { // 해당 구역 요소가 두개 (두 숫자만 비교해서 넣으면 됨)
if (nums[low] > nums[high]) {
int temp = nums[low];
nums[low] = nums[high];
nums[high] = temp;
}
return;
}
// 왼쪽 파트(low ~ mid)와 오른쪽 파트(mid+1 ~ high)를 순회하며 더 작은 숫자부터 temp 배열에 넣음
int lowP = low, highP = mid+1;
int loc = 0;
int *temp = (int *)malloc(sizeof(int) * (high - low + 1));
while ((lowP <= mid) && (highP <= high)) {
if (nums[lowP] < nums[highP]) {
temp[loc] = nums[lowP];
lowP++;
} else {
temp[loc] = nums[highP];
highP++;
}
loc++;
}
// 남은 오른쪽 파트를 배열에 넣음
while (highP <= high) {
temp[loc] = nums[highP];
highP++;
loc++;
}
// 남은 왼쪽 파트를 배열에 넣음
while (lowP <= mid) {
temp[loc] = nums[lowP];
lowP++;
loc++;
}
// temp 배열에 정렬이 완성된 배열을 nums 배열에 복사해넣기
loc = 0;
for (int i = low; i <= high; i++) {
nums[i] = temp[loc];
loc++;
}
free(temp);
}
void mergeSort(int *nums, int low, int high) {
if (low >= high) return;
int mid = (low + high) / 2;
mergeSort(nums, low, mid); // 왼쪽 파트(low~mid) 다시 나누기
mergeSort(nums, mid+1, high); // 오른쪽 파트(mid+1~high) 다시 나누기
merge(nums, low, mid, high); // merge하면서 정렬하기
}
int main() {
int N;
scanf("%d", &N);
int *nums = (int *)malloc(sizeof(int) * N);
for (int i = 0; i < N; i++) scanf("%d", &nums[i]);
mergeSort(nums, 0, N-1);
for (int i = 0; i < N; i++) printf("%d\n", nums[i]);
free(nums);
}
알고리즘의 핵심인 mergeSort() 함수와 merge() 함수를 조금 더 자세히 보겠습니다.
우선 mergeSort() 함수를 보면, 재귀를 통해 배열을 나누는 과정을 구현한 것을 알 수 있습니다.
void mergeSort(int *nums, int low, int high) {
if (low >= high) return;
int mid = (low + high) / 2;
mergeSort(nums, low, mid); // 왼쪽 파트(low~mid) 다시 나누기
mergeSort(nums, mid+1, high); // 오른쪽 파트(mid+1~high) 다시 나누기
merge(nums, low, mid, high); // merge하면서 정렬하기
}
위 코드를 실행하면 아래 그림의 순서처럼 원소가 하나인 배열까지 쪼개졌다가 다시 합쳐지면서 정렬되는 양상을 띄게 됩니다. low와 high 인자를 통해 다룰 배열의 범위를 설정함으로서, 배열을 나눠가는 과정을 구현하는 것입니다. 그리고 함수 처음에 if문으로 low 숫자가 high 숫자보다 크거나 같을 시 함수를 return하면서, 배열 요소가 하나가 되면 재귀를 중단하고 하나씩 return 해가면서 배열을 정렬한다는 것을 알 수 있습니다.
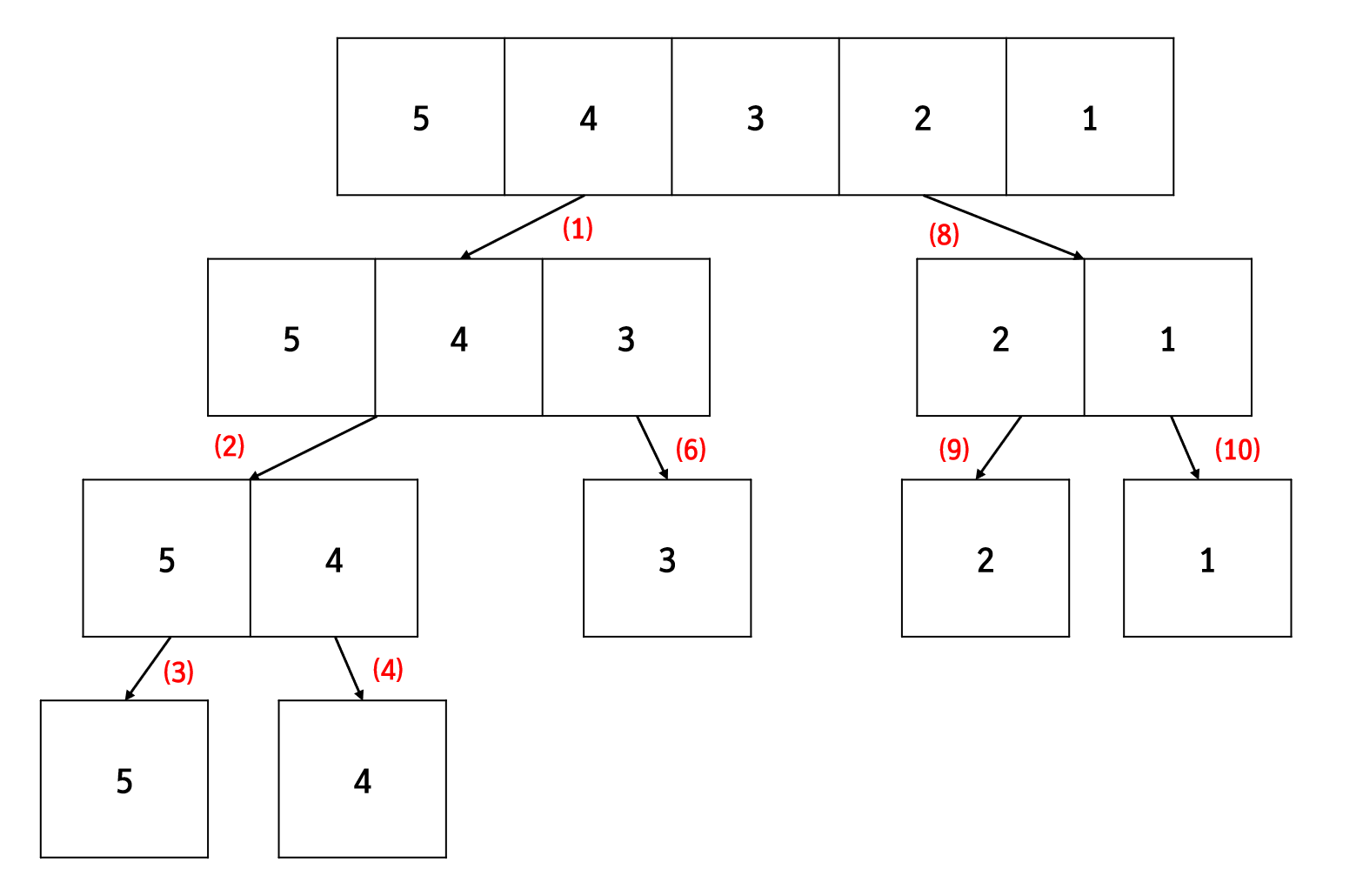
다음으로 merge() 함수를 보면, 주어진 배열 범위의 왼쪽 파트(low부터 mid까지)와 오른쪽 파트(mid+1부터 high까지)를 비교하면서 더 작은 요소를 임시적으로 만든 temp 배열에 넣으면서 정렬하고 있습니다.
우선 if문을 통해 복잡한 과정을 굳이 처리할 필요 없는 주어진 배열 범위 내 요소가 하나인 경우와 두 개인 경우를 먼저 처리하고 return해버립니다. 우선 low와 high가 같은 경우는 주어진 범위 내 요소가 하나라는 것인데, 이렇게 되면 굳이 merge를 통해 정렬할 필요가 없으니 바로 return합니다. 그리고 low와 mid가 같은 경우는, 주어진 범위 내 요소가 두 개라는 것인ㄷ네, 이렇게 되면 임시 배열을 생성하고 오른쪽 파트와 왼쪽 파트를 하나하나 비교하는 복잡한 과정을 처리하는 대신 두 개의 요소만 비교하여 만약 왼쪽 파트에 있는 수가 더 크다면 둘을 교환해주면 되므로, 해당 과정을 처리해주고 return합니다.
이렇게 예외적으로 간단한 경우를 처리해주고 나서, 일반적인 경우에 대한 코드를 작성합니다. 우선 lowP와 highP 함수로각각 왼쪽, 오른쪽 구역을 순회할 포인터를 만들어주고, 정렬된 요소들을 임시적으로 담아둘 temp 배열도 만들어줍니다. 각각 lowP와 highP가 가리키는 배열 내 요소(숫자)를 비교하여, 더 작은 수를 temp에 넣어주고, 넣은 수를 가리키는 포인터는 다음으로 이동시켜줍니다. 왼쪽이나 오른쪽 파트 중 하나라도 다 순회하게 되면 while문을 종료하고, 다음 while문으로 넘어가서 왼쪽이나 오른쪽 파트에 남은 숫자들로 temp 배열을 채워줍니다.
마지막으로 정렬된 temp 배열을 nums 배열 해당 부분에 넣어주면 두 개의 배열 범위를 정렬하여 합치는 merge 과정이 끝나게 됩니다.
void merge(int *nums, int low, int mid, int high) {
if (low >= high) return; // 해당 구역 요소가 하나 (정렬 필요 없음)
else if (low == mid) { // 해당 구역 요소가 두개 (두 숫자만 비교해서 넣으면 됨)
if (nums[low] > nums[high]) {
int temp = nums[low];
nums[low] = nums[high];
nums[high] = temp;
}
return;
}
// 왼쪽 파트(low ~ mid)와 오른쪽 파트(mid+1 ~ high)를 순회하며 더 작은 숫자부터 temp 배열에 넣음
int lowP = low, highP = mid+1;
int loc = 0;
int *temp = (int *)malloc(sizeof(int) * (high - low + 1));
while ((lowP <= mid) && (highP <= high)) {
if (nums[lowP] < nums[highP]) {
temp[loc] = nums[lowP];
lowP++;
} else {
temp[loc] = nums[highP];
highP++;
}
loc++;
}
// 남은 오른쪽 파트를 배열에 넣음
while (highP <= high) {
temp[loc] = nums[highP];
highP++;
loc++;
}
// 남은 왼쪽 파트를 배열에 넣음
while (lowP <= mid) {
temp[loc] = nums[lowP];
lowP++;
loc++;
}
// temp 배열에 정렬이 완성된 배열을 nums 배열에 복사해넣기
loc = 0;
for (int i = low; i <= high; i++) {
nums[i] = temp[loc];
loc++;
}
free(temp);
}
이렇게 두 개의 주요한 함수를 써서 정렬을 해주면, 백준에서도 정답 처리가 되는 모습을 확인할 수 있습니다.

'기초 공부 (언어 및 알고리즘) > 알고리즘 (C언어)' 카테고리의 다른 글
| [백준 9461번/C언어] 파도반 수열, 동적계획법으로 풀이 (2) | 2023.12.10 |
|---|---|
| [백준 2579번/C언어] 계단 오르기, 동적계획법으로 풀이 (3) | 2023.12.09 |
| [백준 2748번/C언어] 피보나치 수, 두 가지 접근법으로 풀기 (2) | 2023.12.08 |
| [백준 1436번/C언어] 영화감독 숌 브루트포스로 풀이 (2) | 2023.12.05 |
| [백준 1018번/C언어] 체스판 다시 칠하기 브루트포스로 풀이 (1) | 2023.12.04 |