백준 1931번 문제를 Merge Sort(합병 정렬)을 이용하여 풀어보았습니다.
백준 1931번: https://www.acmicpc.net/problem/1931
1931번: 회의실 배정
(1,4), (5,7), (8,11), (12,14) 를 이용할 수 있다.
www.acmicpc.net
문제 내용은 다음과 같습니다.
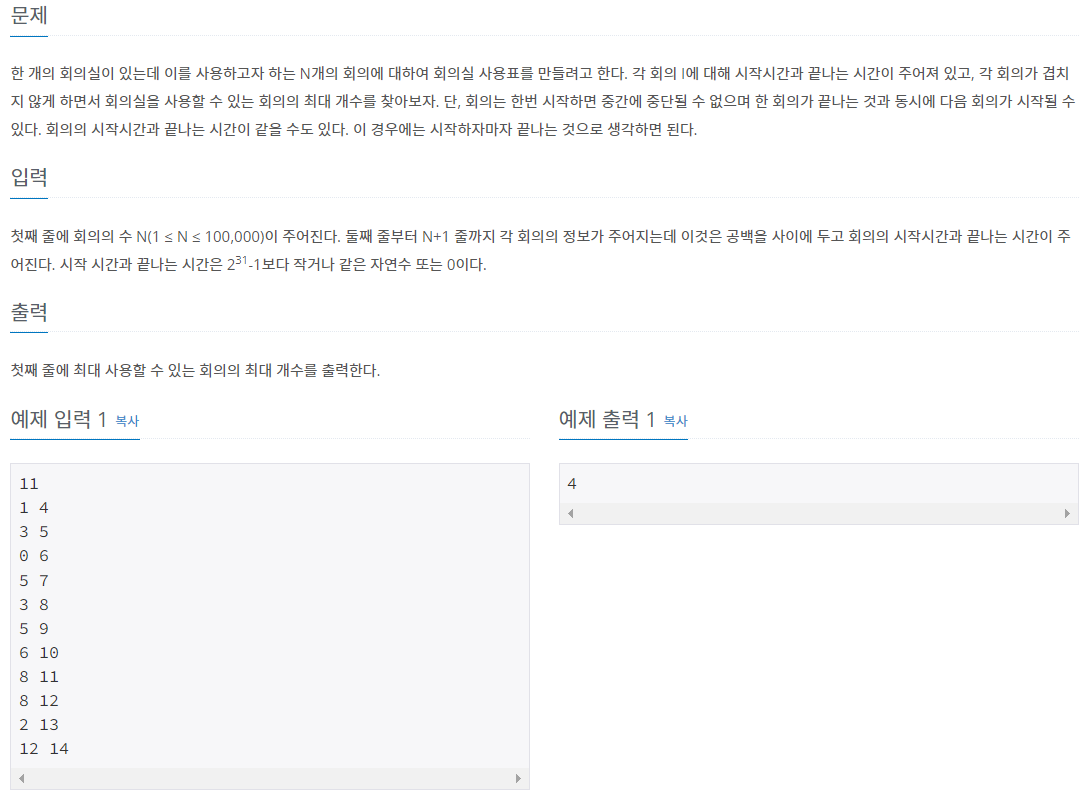
문제 특성상 먼저 정렬을 해준 후 푸는 것이 유리하기 때문에, Merge Sort를 이용하여 정렬을 해준 후 문제를 풀어주었습니다. 원래는 Linked List를 이용해서 정렬을 했는데, O(n^2) 이상의 복잡도가 나와서 시간 초과가 발생했습니다. 따라서 정렬 중 최악의 경우에 가장 효율적일 수 있는 O(n log n)의 복잡도를 가진 Merge Sort를 이용했습니다. Merge Sort에 대한 더 자세한 설명은, 정렬 문제를 풀이한 제 블로그 이전 글에서 확인할 수 있습니다.
https://programming-diary-ina.tistory.com/5
[백준 2751번/C언어] 수 정렬하기, Merge Sort로 풀이
백준 2751번 문제를 Merge Sort로 풀어보았습니다. 처음에는 Quick Sort로 풀이했으나, 계속 정답처리 되지 않아 찾아보니 Quick Sort는 거꾸로 정렬되어 있을 경우 O(N^2)의 시간복잡도가 발생하기 때문에
programming-diary-ina.tistory.com
문제를 푼 대략적인 방법을 먼저 설명하겠습니다. 우선 회의가 끝나는 시간을 기준으로 내림차순으로 정렬을 합니다. 만약 회의가 끝나는 시간이 같다면 회의가 시작하는 시간이 큰 순서대로 정렬합니다. 그리고 정렬된 리스트를 순회하면서, 현재 순회 중인 요소의 끝나는 시간이 앞서 선택되었던 회의의 시작 시간보다 작거나 같다면 해당 회의도 진행할 수 있는 것이므로 카운트를 늘려나가는 방식입니다. 또한, 만약 순회하다가 이전에 선택되었던 회의보다 더 나은 선택지(시작하는 시간이 더 늦은 선택지)가 있다면 해당 선택지로 선택을 바꾼 후 순회를 계속합니다. 예시를 통해 보면 아래 사진과 같습니다.

우선 이미 끝나는 시간의 내림차순 순서로 정렬이 되어있고, [10, 12]와 [8, 12]와 같이 끝나는 시간이 같다면 시작 시간이 큰 순으로 정렬이 되어 있는 상태에서 시작합니다.
첫 번째인 [12, 14]의 경우에는 아직 확정된 회의가 아니므로 선택하고 넘어갑니다. 그 이후부터는 이전에 선택된 회의의 시작시간보다, 현재 확인 중인 회의의 끝나는 시간이 더 작거나 같다면 해당 회의를 선택할 수 있습니다.
만약 이 기준을 바탕으로 선택될 수 없는 회의이지만, 이미 선택된 회의보다 시작시간이 늦다면, 이는 현재 확인 중인 회의가 더 유리하다는 것을 의미합니다. 이미 순회한 회의들의 끝나는 시간이 현재 확인 중인 회의에 비해 늦으므로 (내림차순으로 정렬되어 있기 때문에 해당 내용이 보장) 시작 시간이 늦다면 회의시간이 짧을 수밖에 없습니다. 따라서 해당 이전에 선택한 회의의 선택을 취소해 주고, 지금 확인 중인 회의로 선택을 바꿔주면 됩니다. 이때, count의 경우 -1 +1이므로 바꿔줄 필요가 없고, 이전에 선택된 시작 시간만 바꿔주면 됩니다. 빨간색 펜으로 써져 있는 내용이 여기에 해당합니다.
이런 과정을 끝까지 반복하다보면, 최종 output인 5를 도출해 낼 수 있습니다.
그렇다면 위 내용을 구현한 코드를 살펴보겠습니다. 우선 회의에 대한 정보는 시작시간과 끝나는 시간, 두 개의 값이 필요하므로 이를 구조체로 정의해 주었습니다. 구조체 내 start가 시작 시간을 담는 변수, end가 끝나는 시간을 담는 변수에 해당합니다.
typedef struct MEETING {
int start;
int end;
} Meeting;
그리고 end 정보의 내림차순 정렬을 위한 MergeSort() 함수를 정의해주었습니다. Merge Sort는 주로 Recursive Function으로 구현됩니다. 대략적인 흐름은 자료를 왼쪽 부분과 오른쪽 부분으로 나누어서 모두 정렬한 후 두 개를 다시 합치는 것입니다. 한 부분 내 원소가 하나가 될 때까지 계속 나눠서 그 부분을 먼저 정렬하고, 정렬된 두 개의 부분을 양쪽 부분에서 더 큰 값부터 넣으며 다시 합치면서 정렬한다는 원리입니다. 더 자세한 설명은 앞서 언급한 대로 제 블로그 앞선 글에서 확인 가능합니다. 여기서는 코드 구현에 대해서 더 집중적으로 언급하겠습니다.
우선 함수가 input으로 받는 인자를 보겠습니다. l 변수는 정렬해야 할 target part의 시작 index, r은 끝 index에 해당합니다. timeTable은 우리가 정렬해야 할 배열의 메모리입니다. 바뀐 배열을 main 함수에서도 적용되게 해야 하므로 메모리 값으로 받아 two pointer가 이용되었습니다.
함수 시작에서는, 재귀함수로 사용될 것이기 때문에 재귀 중단 조건을 먼저 작성해주어야 합니다. 시작 index인 l이 끝 index인 r보다 크거나 같다는 것은 정렬해야 할 target part 내 원소가 하나이거나 없다는 것을 의미합니다. 따로 정렬할 것이 없다는 뜻이므로 바로 return 해줍니다. 그리고 r - l 이 1인 경우에는 원소가 2개라는 뜻이기 때문에, 더 복잡한 아래 과정을 거치기보다는 그 두 개만 비교해서 r 위치의 원소가 더 앞에 있어야 하는 경우(end가 더 크거나 end는 같지만 start가 더 큰 경우)만 두 개의 순서를 바꿔주면 됩니다.
그리고 이제 본격적으로 Merge Sort를 진행해주면 된다. 우선 왼쪽 부분과 오른쪽 부분으로 나누고, 나뉜 부분의 정렬이 완료되면 그 둘을 merge 해주며 정렬을 완료하게 됩니다. 나눌 때는 중앙값을 구해주고, l에서 중앙값까지와 중앙값+1에서 r까지를 다시 구간으로 설정하여 함수를 실행해 줍니다. 이 두 함수 실행이 완료되면, 두 구간은 각각 정렬이 완료되었다는 뜻입니다.
그리고 나면 정렬이 완료된 두 구간을 merge해줍니다. 우선 두 구간을 합쳐 담을 배열을 하나 선언해 주고, 여기에 정리한 후 다시 원래 배열에 옮겨담으면 됩니다. 양쪽 배열의 첫 번째 원소부터 시작하여 둘 중 더 앞에 나와야 하는 원소부터 새로운 배열인 m에 담아주면 됩니다. 하나씩 차례로 담다가 양쪽 중 하나가 먼저 다 담기면, 다른 남아있는 원소를 다시 차례로 넣어줍니다. 마지막으로 m에 정렬된 원소들로 timeTable 배열을 다시 채워주면 l부터 r까지 구간의 정렬이 완성됩니다.
void MergeSort(int l, int r, Meeting **timeTable) {
if (l >= r) return; // 더 이상 정렬이 필요 없음
if (r - l == 1) { // 구간 내 원소가 2개 뿐일 때
if ((*timeTable)[l].end == (*timeTable)[r].end) {
if ((*timeTable)[l].start < (*timeTable)[r].start) {
Meeting temp = (*timeTable)[l];
(*timeTable)[l] = (*timeTable)[r];
(*timeTable)[r] = temp;
}
} else if ((*timeTable)[l].end < (*timeTable)[r].end) {
Meeting temp = (*timeTable)[l];
(*timeTable)[l] = (*timeTable)[r];
(*timeTable)[r] = temp;
}
return;
}
int mid = (l + r) / 2;
MergeSort(l, mid, timeTable); // 왼쪽 구간
MergeSort(mid+1, r, timeTable); // 오른쪽 구간
// 왼쪽과 오른쪽 구간 merge
Meeting *m = (Meeting *)malloc(sizeof(Meeting) * (r - l + 1));
if (m == NULL) return;
int i = 0, j = mid + 1, left = l;
while (l <= mid && r >= j) {
if ((*timeTable)[l].end == (*timeTable)[j].end) {
if ((*timeTable)[l].start > (*timeTable)[j].start)
m[i++] = (*timeTable)[l++];
else m[i++] = (*timeTable)[j++];
} else if ((*timeTable)[l].end > (*timeTable)[j].end)
m[i++] = (*timeTable)[l++];
else m[i++] = (*timeTable)[j++];
}
while (l <= mid) m[i++] = (*timeTable)[l++];
while (r >= j) m[i++] = (*timeTable)[j++];
for (i = left; i <= r; i++) (*timeTable)[i] = m[i-left];
free(m);
}
마지막으로 메인 함수입니다. 우선 회의 정보를 담을 timeTable 배열을 만들어 여기에 회의 정보(시작 시간과 끝나는 시간)를 입력받습니다. 입력받은 배열을 앞서 만든 MergeSort() 함수에 넣어 정렬을 하고, 본격적으로 가능한 최대 회의 개수를 세어주면 됩니다.
앞서 언급한 대로, 이전에 선택된 회의의 시작시간과 같거나 이른 종료시간을 가진 회의만 선택 가능하므로 curEnd 변수에 이전 함수에 start를 저장해주어서 현재 end에 대한 조건을 확인할 수 있게 합니다. count 변수는 몇 개의 회의를 넣을 수 있는지 세어줄 변수입니다. 앞서 언급한 대로, 첫 번째 회의를 넣을 때는 이미 선택된 회의가 없으므로 무조건 선택이 가능합니다. 따라서 for문을 시작하기 전에 첫 번째 회의의 시작 시간을 curEnd 변수에 넣어주고, count의 초기값을 1로 넣어준 후, for문을 두 번째 회의부터 순회합니다.
for문 내에서 정렬된 회의 정보들을 순회하면서, 만약 현재 확인 중인 회의의 종료시간이 curEnd 변수에 저장된 수보다 작거나 같다면, 해당 회의를 선택해야 하므로 count를 증가시켜주고, curEnd를 현재 회의의 시작시간으로 바꿔줍니다. 만약 회의를 선택할 수 없지만, 현재 회의가 이전에 선택했던 회의보다 유리하다면(현재 회의의 끝나는 시간은 더 작지만 시작시간이 더 큰 경우), 현재 회의의 시작 시간으로 curEnd를 바꿔주고 넘어갑니다.
이렇게 순회를 마치고 나면 count 변수에 가능한 최대 회의 개수가 담기게 됩니다. 이를 출력해주면 프로그램이 마무리됩니다.
int main() {
int N;
scanf("%d", &N);
// 회의 정보 입력받기
Meeting *timeTable = (Meeting *)malloc(sizeof(Meeting) * N);
if (timeTable == NULL) return 1;
int s, e;
for (int i = 0; i < N; i++) {
scanf("%d%d", &s, &e);
timeTable[i].start = s;
timeTable[i].end = e;
}
// 회의 정보 정렬
MergeSort(0, N-1, &timeTable);
// 최대 회의 개수 찾기
int curEnd = timeTable[0].start;
int count = 1;
for (int i = 1; i < N; i++) {
if (timeTable[i].end <= curEnd) { // 회의 추가가 가능한 경우
count++;
curEnd = timeTable[i].start;
} else if (curEnd < timeTable[i].start) { // 추가가 불가능하지만 현재 회의가 더 유리한 경우
curEnd = timeTable[i].start;
}
}
free(timeTable);
printf("%d", count);
}
전체 코드는 아래와 같습니다.
#include <stdio.h>
#include <stdlib.h>
typedef struct MEETING {
int start;
int end;
} Meeting;
void MergeSort(int l, int r, Meeting **timeTable) {
if (l >= r) return;
if (r - l == 1) {
if ((*timeTable)[l].end == (*timeTable)[r].end) {
if ((*timeTable)[l].start < (*timeTable)[r].start) {
Meeting temp = (*timeTable)[l];
(*timeTable)[l] = (*timeTable)[r];
(*timeTable)[r] = temp;
}
} else if ((*timeTable)[l].end < (*timeTable)[r].end) {
Meeting temp = (*timeTable)[l];
(*timeTable)[l] = (*timeTable)[r];
(*timeTable)[r] = temp;
}
return;
}
int mid = (l + r) / 2;
MergeSort(l, mid, timeTable);
MergeSort(mid+1, r, timeTable);
Meeting *m = (Meeting *)malloc(sizeof(Meeting) * (r - l + 1));
if (m == NULL) return;
int i = 0, j = mid + 1, left = l;
while (l <= mid && r >= j) {
if ((*timeTable)[l].end == (*timeTable)[j].end) {
if ((*timeTable)[l].start > (*timeTable)[j].start)
m[i++] = (*timeTable)[l++];
else m[i++] = (*timeTable)[j++];
} else if ((*timeTable)[l].end > (*timeTable)[j].end)
m[i++] = (*timeTable)[l++];
else m[i++] = (*timeTable)[j++];
}
while (l <= mid) m[i++] = (*timeTable)[l++];
while (r >= j) m[i++] = (*timeTable)[j++];
for (i = left; i <= r; i++) (*timeTable)[i] = m[i-left];
free(m);
}
int main() {
int N;
scanf("%d", &N);
Meeting *timeTable = (Meeting *)malloc(sizeof(Meeting) * N);
if (timeTable == NULL) return 1;
int s, e;
for (int i = 0; i < N; i++) {
scanf("%d%d", &s, &e);
timeTable[i].start = s;
timeTable[i].end = e;
}
MergeSort(0, N-1, &timeTable);
int curEnd = timeTable[0].start;
int count = 1;
for (int i = 1; i < N; i++) {
if (timeTable[i].end <= curEnd) {
count++;
curEnd = timeTable[i].start;
} else if (curEnd < timeTable[i].start) {
curEnd = timeTable[i].start;
}
}
free(timeTable);
printf("%d", count);
}'기초 공부 (언어 및 알고리즘) > 알고리즘 (C언어)' 카테고리의 다른 글
| [백준 10845/C언어] 큐 풀이 (6) | 2024.04.15 |
|---|---|
| [백준 10816/C언어] 숫자 카드 2 풀이 (1) | 2024.04.14 |
| [백준 14501번/C언어] 퇴사, 동적계획법(DP, Dynamic Programming)으로 풀이 (2) | 2024.04.11 |
| [백준 1697번/C언어] 숨바꼭질 풀이 (1) | 2024.04.10 |
| [백준 2667번/C언어] 단지번호붙이기 풀이 (0) | 2024.04.08 |