백준 12865번 문제를 Dynamic Programming (DP, 동적 계획법)을 이용하여 풀어보았습니다. 이 문제는 대표적인 냅섹 문제(KnapSack Problem)에 해당합니다.
백준 12865번: https://www.acmicpc.net/problem/2748
2748번: 피보나치 수 2
피보나치 수는 0과 1로 시작한다. 0번째 피보나치 수는 0이고, 1번째 피보나치 수는 1이다. 그 다음 2번째 부터는 바로 앞 두 피보나치 수의 합이 된다. 이를 식으로 써보면 Fn = Fn-1 + Fn-2 (n ≥ 2)가
www.acmicpc.net
문제 내용은 다음과 같습니다.
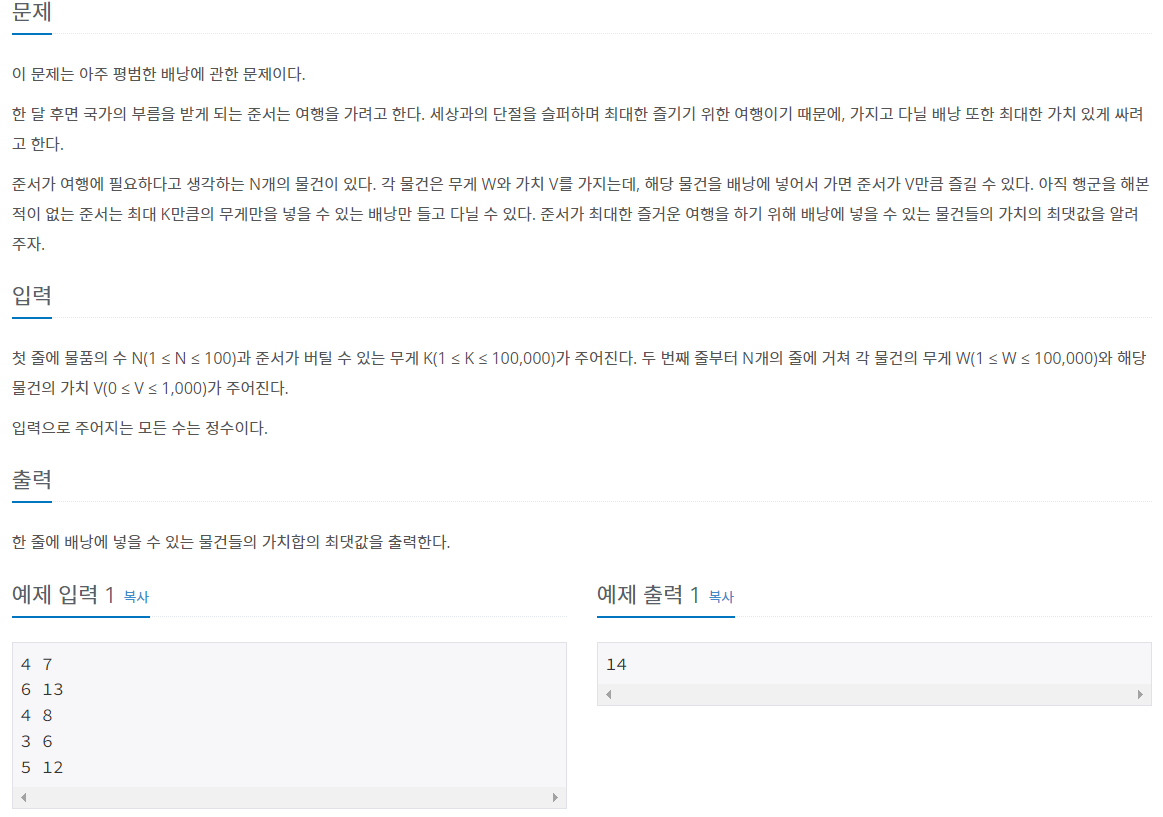
이 문제는 앞서 언급한 대로 동적계획법으로 푸는 문제입니다. 혹시 동적 계획법이 익숙하지 않은 분들이라면 더 쉬운 동적계획법 문제부터 차근히 풀어보시는 것을 추천드립니다. 동적계획법을 사용하지 않아도 작동하게 할 수는 있지만, 아마 시간효율성 측면에서 불리하여 백준에서 통과하지는 못할 것입니다.
저는 2차원 배열의 동적 배열을 저장하여 문제를 해결했습니다. dp[x][y]의 배열이 제가 만든 동적 배열이라고 하면, x 자리는 현재 확인하고 있는 배낭의 부피입니다. 그래서 1부터 문제에서 주어지는 부피까지를 저장하는 배열이 될 것입니다. y 자리는 y번째 물건까지 확인한 상황을 나타냅니다. 따라서 dp[x][y]에 저장된 값은 크기가 x인 배낭에 y물건까지 체크하고 넣었을 때의 최대 가치가 됩니다.
그렇다면 배열 각각의 자리에 들어갈 최대 가치를 구할 때는 어떤 점화식을 써야 할까요? 저는 아래와 같은 점화식을 세워 문제를 해결했습니다.
F(x, y) = Max(F(x - weight[y], y-1) + value[y], F(x, y-1))
점화식에서 파악할 수 있듯, 두 가지 경우 중 더 큰 경우를 선택하여 배열에 저장하는 방식입니다. 첫 번째 경우는 F(x - weight[y], y-1) + value[y] 입니다. 이 경우는 현재 체크하고 있는 배낭 부피, 즉 물건이 들어갈 수 있는 최대 무게(x)에서 현재 체크하고 있는 물건의 무게(weight[y])를 뺀 무게, 즉 남은 무게(x - weight[y])를 새롭게 체크하는 무게로 설정하여, 해당 무게에서 현재 물건 이전까지 체크했을 때의 최댓값에, 현재 물건의 가치(value[y])를 더해줍니다. 즉, 현재 물건을 넣고 나면, x - weight[y] 만큼 빈 공간이 남게 되니까 그 공간에 넣을 수 있는 최대 가치를 더해주면, 현재 확인하고 있는 물건을 포함한다고 가정했을 때 가질 수 있는 최댓값이 될 것입니다.
두 번째 경우는 F(x, y-1) 입니다. 이 경우는 그냥 바로 이전 배열 요소를 그대로 가져오는 것입니다. 남은 무게가 0이나 음수인 경우는 현재 물건을 넣을 수 없다는 의미이므로 앞선 경우를 적용할 수 없습니다. 혹은 앞선 경우를 적용할 수 있으나, 이전 요소를 그대로 가져오는 것이 더 큰 값이 적용될 수 있습니다.
이렇게 점화식을 통해, dp[x][y]에 위치에 맞는 값을 저장하고, 최종적으로 도출하고자 하는 답에 해당하는 dp{M][N]까지 찾아주면 문제를 해결할 수 있습니다.
위 점화식을 바탕으로 코드를 작성하였습니다. makeDpAry() 함수는 동적 배열을 만들기 위한 동적 할당을 하는 과정으로 물건의 개수와 배낭의 크기에 맞는 크기의 2차원 배열을 만들어서 모든 값을 0으로 초기화해 주는 함수입니다. 메인 함수가 너무 길어지길래 따로 뺀 것이고 특별한 건 없기 때문에 넘어가겠습니다.
메인 함수는 문제에서 주어진 대로, 물건의 개수(N)과 버틸 수 있는 무게(M)를 입력받는 것으로 시작합니다. 이를 바탕으로 물건의 무게정보를 담을 wei 배열과 가치 정보를 담을 val 배열을 각각 동적할당으로 만들어줍니다. 이후에는 만들어둔 함수로 결괏값을 저장할 dp 배열을 생성하고, 본격적으로 배열을 채우며 답을 찾는 과정을 시작합니다. 최종 결과값은 dp[M][N-1] 위치에 저장될 것입니다. (M의 무게 + N번째 물건까지 체크)
우선 이중 반복문으로 i는 현재 i의 무게를 가진 부피를 체크하고 있는 것(행)을 의미할 것이고, j는 j번째 물건을 확인하고 있는 것(열)을 의미하게 됩니다. 이중 루프 내에서는 각각 조건에 따라서 배열을 하나씩 채워나갑니다.
첫번째 조건은 j가 0일 때인데요, 위 점화식에서 확인할 수 있듯, 점화식에서는 모두 이전 열의 값을 참고하여 현재 값을 도출해 냅니다. 하지만 j가 0이면 첫 번째 열에 해당하므로 참고할 이전 열이 없습니다. 따라서 만약 첫 번째 물건이 현재 무게보다 작거나 같다면 해당 물건 하나를 배낭에 넣는 것으로 시작할 수 있으므로 해당 물건의 가치를 배열에 저장해 주고, 아니라면 아무것도 넣지 않은 상태로 시작해야 하므로 0을 배열에 저장해 줍니다.
j가 0이 아닌 경우에는, 우선 확인 중인 배낭의 부피에서 현재 물건의 무게를 뺀 값이 0보다 크다는 것은 현재 물건이 배낭에 들어갈 남은 무게가 충분하다는 뜻입니다. 따라서 앞선 점화식에서 봤던 F(x - weight[y], y-1) + value[y] 을 적용해 주면 됩니다. 만약 해당 조건이 충족이 안된다면 dp[i][j]는 0으로 남아있을 것입니다. 따라서 위 조건에 해당되지 않거나, 위 조건으로 계산한 값이 dp[i][j-1] 즉 이전 물건까지 확인한 값보다 작다면, dp[i][j-1]이 dp[i][j]에도 적용될 것입니다.
마지막으로 도출되는 답에 해당하는 dp[M][N-1]을 출력하고, 동적 할당한 배열들을 해제해 주는 것으로 프로그램을 마무리하게 됩니다.
#include <stdio.h>
#include <stdlib.h>
int **makeDpAry(int N, int M) {
int **dp = (int **)malloc(sizeof(int*) * (M + 1));
if (dp == NULL) return NULL;
for (int i = 0; i <= M; i++) {
dp[i] = (int *)malloc(sizeof(int) * N);
if (dp[i] == NULL) {
for (int j = 0; j < i; j++) free(dp[j]);
free(dp);
return NULL;
}
for (int j = 0; j < N; j++) dp[i][j] = 0;
}
return dp;
}
int main() {
int N, M;
scanf("%d%d", &N, &M);
int *wei = (int *)malloc(sizeof(int) * N);
int *val = (int *)malloc(sizeof(int) * N);
if (wei == NULL || val == NULL) return 1;
for (int i = 0; i < N; i++) scanf("%d%d", &(wei[i]), &(val[i]));
int **dp = makeDpAry(N, M);
if (dp == NULL) return 1;
for (int i = 1; i <= M; i++) {
for (int j = 0; j < N; j++) {
if (j == 0) {
if (i >= wei[j]) dp[i][j] = val[j];
else dp[i][j] = 0;
} else {
if ((i - wei[j]) >= 0)
dp[i][j] = dp[i - wei[j]][j-1] + val[j];
if (dp[i][j] < dp[i][j-1])
dp[i][j] = dp[i][j-1];
}
}
}
printf("%d", dp[M][N-1]);
for (int i = 0; i <= M; i++) free(dp[i]);
free(dp);
}'기초 공부 (언어 및 알고리즘) > 알고리즘 (C언어)' 카테고리의 다른 글
| [백준 2667번/C언어] 단지번호붙이기 풀이 (0) | 2024.04.08 |
|---|---|
| [백준 2164번/C언어] 카드2 풀이 (2) | 2024.04.07 |
| [백준 10699번/C언어] 오늘 날짜 풀이 (1) | 2024.04.02 |
| [백준 1012번/C언어] 괄호 풀이 (1) | 2024.03.22 |
| [백준 10828번/C언어] 스택 풀이 (1) | 2024.03.21 |