[Recursion] Hanoi Tower 만들기

본격적으로 자료구조 공부를 시작하기 전 첫 번째로 구현했던 코드입니다. 

백준 1914번 '하노이탑' 문제와도 연관이 있을 수 있으나, 백준에 맞춰 작성한 것은 아니므로 그대로 넣을 시 백준에서 오답처리됩니다. 이 코드를 기반으로 백준도 풀어보았으니, 기회가 된다면 업로드하도록 하겠습니다. 

 

 

 

문제를 먼저 소개해본다면, 3개의 rods가 있고, n개의 disks가 있을 때, 다음과 같은 조건을 충족하면서 첫 번째 rod에 있는 모든 disk들을 세 번째 rod로 옮기는 것이 해결해야 할 문제입니다. 

[조건 1] 한 번에 한 개의 disk만 옮길 수 있다.
[조건 2] '움직인다'라는 것은 선택한 rod의 가장 상단에 있는 disk를 옮기는 것을 말한다
[조건 3] 더 큰 disk를 더 작은 disk 위에 위치시킬 수 없다.

 

 

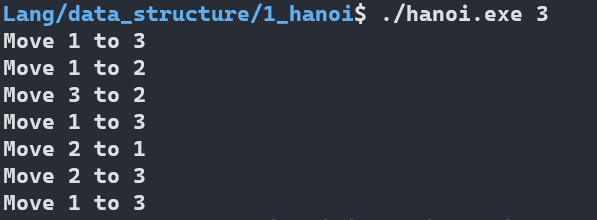
결과적으로 input으로 disk의 개수인 n을 입력받아, 아래와 같이 몇번째 rod에서 몇 번째 rod로 이동했는지를 순서대로 print 하는 것을 목표로 합니다. (disk의 개수가 0일 경우 0 출력)

input이 3일 때의 output

 

 

 

 

전체 코드를 먼저 소개하면 다음과 같습니다. 오류가 있을 수 있으니, 참고하시어 보시고, 혹여나 오류를 발견하신다면 댓글로 알려주시면 감사하겠습니다.

#include <stdio.h>
#include <stdlib.h>

int hanoi(int from, int mid, int to, int disk)
{
    if (disk == 1) 
    {
        printf("Move %d to %d\n", from, to);
        return 0;
    }
    
    hanoi(from, to, mid, disk-1);
    printf("Move %d to %d\n", from, to);
    hanoi(mid, from, to, disk-1);
    return 0;
}

int main(int argc, char **argv)
{
    if (argc != 2)
    {
        printf("Correct Usage : [program] [number of disks]\n");
        return 0;
    }

    int disk = atoi(argv[1]);
    if (disk == 0) return 0;
    else hanoi(1, 2, 3, disk);
}

 

위에서 기본적인 내용은 빼고 핵심 알고리즘만 정리해서 설명하도록 하겠습니다.

 

 

 

우선 hanoi 함수를 자세히 살펴보겠습니다. 이 함수는 해당 코드의 핵심 함수로, 이 함수를 재귀적으로 사용하여 문제를 해결했습니다. 

int hanoi(int from, int mid, int to, int disk)

인자(Argument)를 먼저 살펴보면, 4개의 integer 값을 받고 있습니다.

여기서 from은 disk를 꺼내서 옮길 rod를 말하고, to는 from에서 꺼낸 디스크를 옮겨놓을 target rod를 말합니다. mid는 당연히 아무것도 하지 않는 남는 rod가 되겠죠. (아무것도 하지 않는 mid를 굳이 인자로 받는 이유는 재귀하는 과정에서 mid rod를 사용하게 되기 때문입니다. 코드를 끝까지 익히시면 자연히 이해하게 되실 것입니다.) 저는 rod를 각각 1, 2, 3으로 표현하여 인자로 받았습니다. (출력할 때도 같은 방식으로 합니다.)

그리고 마지막 인자인 disk의 경우는 disk의 개수입니다. 초기값은 input으로 받은 값이 되겠고, 이후에는 disk를 다 옮겼을  때 재귀를 종료할 목적으로 사용됩니다. 

if (disk == 1) 
{
    printf("Move %d to %d\n", from, to);
    return 0;
}

다음은 재귀를 종료하는 목적의 if문입니다. 인자로 받은 disk가 하나 남게 되면, 마지막으로 한 번  from rod에서 to rod로 disk를 움직인 후, return으로 재귀를 종료하게 됩니다.

hanoi(from, to, mid, disk-1);
printf("Move %d to %d\n", from, to);
hanoi(mid, from, to, disk-1);
return 0;

hanoi 함수의 마지막 부분입니다. 바로 hanoi 함수를 재귀적으로 사용하는 부분인데, 첫번째 재귀는 from에서 mid rod로 디스크가 가는 것으로 되어있습니다. 즉, mid rod가 to 인자로 가게 되는 것이죠. 

두 번째 재귀는 mid에서 to로 가는 것으로 되어있습니다.

그리고 두 가지 재귀 함수 모두에서 disk 개수를 하나씩 줄이고 있고, 두 재귀 함수 사이에 from에서 to로 disk를 하나 이동시켜 줍니다.

 

 

다음은 main 함수입니다.

int main(int argc, char **argv)
{
    if (argc != 2)
    {
        printf("Correct Usage : [program] [number of disks]\n");
        return 0;
    }

    int disk = atoi(argv[1]);
    if (disk == 0) return 0;
    else hanoi(1, 2, 3, disk);
}

main 함수에서는 처음 시작할 때 첫 번째 rod에서 세 번째 rod로 이동한다는 것만 아시면 됩니다. 그 외에는 프로그램 처리와 관련된 부분이고 알고리즘과 관련된 주요한 내용은 아니기 때문에 넘어가겠습니다.

 

 

 

코드를 부분 부분 살펴보았는데요, 이렇게 부분적으로 봐서는 큰 알고리즘이 이해가 안 될 수 있습니다. 위에서는 간단한 코드 구성 설명이었고 본격적으로 알고리즘이 어떻게 돌아가는지를 설명해 보겠습니다.

 

우선 disk개수가 3일 때를 예를 들어, 그림으로 한번 보여드리면서 규칙을 찾아보겠습니다. 

초기 상태에서는 아래와 같이 크기 순서대로 첫 번째 rod에 disk 세 개가 모두 모여있습니다. 

disk의 개수가 3일 때 초기 상태

 

이후 첫번째 move는 rod1에서 rod3으로 가장 작은 disk를 옮기게 됩니다.

[First Movement] rod1 to rod3

 

두 번째는 rod1에서 rod2로 두 번째로 작은 disk를 옮기게 되는데, 여기서 주의할 점은 해당 disk는 rod3에 있는 disk보다 크기 때문에 rod3으로는 옮길 수 없다는 점입니다.

[Second Movement] rod1 to rod2

 

세 번째로는 rod3에 있는 가장 작은 disk를 rod2로 옮깁니다. 가장 작은 disk이기 때문에 rod1로 옮길 수도 있지만, 그렇게 되면 가장 큰 disk를 움직일 수 없고, 가장 큰 disk가 rod3으로 가장 먼저 가는 것이 효율적이기 때문에 두 번째로 작은 disk가 있는 rod2로 옮기는 것이 효율적입니다.

[Third Movement] rod3 to rod2 (그림 속 텍스트 화살표 방향에 오류가 있지만, 3에서 2로 가는 것이 맞습니다.)

 

이제 가장 큰 disk를 rod3으로 옮겨줍니다. 이 이후에는 위에서 했던 것과 같은 방식으로 rod2에 있는 두 개의 disk들을 rod3으로 옮겨줍니다. 

[Fourth Movement] rod1 to rod3

 

 

 

위 과정을 정리하면 아래와 같은 순서로 disk들이 옮겨진다는 것을 알 수 있습니다. 

Move 1 to 3
Move 1 to 2
Move 3 to 2
Move 1 to 3
Move 2 to 1
Move 2 to 3
Move 1 to 3

 

자 그림 이제 여기서 규칙을 찾아보겠습니다. 규칙을 찾기 위해서는 하나하나의 움직임에 집중하기보단 큰 흐름 상 disk들이 어디로 향하고 있는지를 파악하는 게 중요합니다. 

 

움직임을 쪼개어 봅시다. 아래 움직임을 자세히 살펴보면, 큰 흐름 상 가장 작은 두 개의 disk들을 rod1에서 rod2로 움직이려 한다는 것을 알 수 있습니다. 

Move 1 to 3
Move 1 to 2
Move 3 to 2

 

가장 작은 두 개의 disk들을 성공적으로 옮겼다면, 가장 큰 디스크를 rod1에서 rod3으로 옮겨줍니다.

Move 1 to 3

 

마지막으로 가장 작은 두 개의 디스크를 rod2에서 rod3으로 옮겨주면 완성입니다.

Move 2 to 1
Move 2 to 3
Move 1 to 3

 

자 이런 큰 흐름으로 다시 코드를 보면, 

초기 메인 함수의 hanoi(1, 2, 3, disk)는 3개의 로드를 rod1에서 3으로 옮기겠다는 초기값이 되겠죠

그리고 hanoi 함수 내 첫 번째 recursion인 hanoi(from, to, mid, disk-1)은 우리가 두 개의 가장 작은 디스크를 rod1에서 rod2로 옮겨줬던 과정을 말할 것입니다. 초기값이 from이 첫 번째 rod, mid가 두 번째 rod인 상황이니 위와 같은 재귀함수로 우리의 목적대로 실행시킬 수 있겠죠.

그리고 printf("Move %d to %d\n", from, to)를 통해 가장 큰 디스크를 rod1에서 rod3으로 옮겨주는 것을 구현합니다.

마지막으로 rod2로 옮겨줬던 가장 작은 두 개의 disk들을 rod3으로 옮겨주는 과정을 hanoi(mid, from, to, disk-1)로 구현해 주면 끝입니다. 

 

재귀함수로 이런 규칙을 디스크 수를 작게 쪼개어 반복해 주는 것으로 이해하면 됩니다. 

개수를 늘려 직접 도전해 보아도 개수가 쪼개지고 쪼개져 같은 과정이 반복된다는 것을 알 수 있습니다.

 

 

 

여기까지 hanoi 예제를 c언어로 구현해 보았습니다.

마지막으로 혹시 코드에 오류가 있거나 제 코드에서 이해가 되지 않으시는 부분이 있다면 댓글 남겨주시면 감사하겠습니다.